The Gauge Integral: Why Henstock–Kurzweil Deserves a Course
The gauge integral, also called the Henstock–Kurzweil integral, is a modification of the Riemann integral that replaces a single fixed tolerance with a variable “gauge” function. This one change produces an integral that includes the ordinary Riemann integral, most improper Riemann integrals, and the Lebesgue integral as special cases, while remaining almost as simple to define as the Riemann integral itself.
Table of Contents
Key Takeaways
- The gauge integral is also known as the Henstock–Kurzweil integral, the narrow Denjoy integral, the Luzin integral, or the Perron integral.
- A function is Lebesgue integrable if and only if it is gauge integrable and its absolute value has a finite gauge integral.
- The improper Riemann integral of sin(x)/x from 0 to infinity equals π/2, even though this function is not Lebesgue integrable in the absolute sense.
- Under the gauge integral, the fundamental theorem of calculus holds even if the derivative fails to exist at countably many points, with no requirement that the derivative be Riemann integrable.
- R. G. Bartle’s book “A Modern Theory of Integration” is devoted entirely to building the gauge integral from first principles.
What Is the Riemann Integral? Two Equivalent Viewpoints
The Riemann integral is defined for a function f mapping the interval [a,b] to the real numbers. It can be constructed in two equivalent ways: the Darboux method and the Riemann sum method.
The Darboux method bounds the area under f from below and above using a partition X = {x₀, x₁, …, xₙ}, where x₀ = a, xₙ = b, and each xᵢ ≤ xᵢ₊₁. The upper and lower Darboux sums are defined as:
[tex]U_X(f) = \sum_{i=0}^{n-1} (x_{i+1} – x_i)\sup_{x\in [x_i,x_{i+1}]}f(x)[/tex]
[tex]L_X(f) = \sum_{i=0}^{n-1} (x_{i+1} – x_i)\inf_{x\in [x_i,x_{i+1}]}f(x)[/tex]
The Darboux integral exists when the difference U_X(f) − L_X(f) approaches zero as the partition X becomes finer. When this happens, the common limit of U_X(f) and L_X(f) is called the Darboux integral.
The second viewpoint uses Riemann sums directly. Given the same partition points and sample points aᵢ chosen so that xᵢ ≤ aᵢ ≤ xᵢ₊₁, the Riemann integral of f is the limit of the sum:
[tex]\sum_{i=0}^{n-1} f(a_i)(x_{i+1} – x_i)[/tex]
as the mesh of the partition tends to zero. The Darboux and Riemann sum approaches produce equivalent results. Ethan Bloch’s textbook Real Numbers and Real Analysis gives a full treatment of this equivalence.
How Are Improper Riemann Integrals Defined?
The Riemann integral extends naturally to unbounded domains such as [a, +∞). For example, the improper integral over this domain is defined as:
[tex]\int_a^{+\infty} f(x)\,dx = \lim_{d\rightarrow +\infty} \int_a^d f(x)\,dx[/tex]
This limit is used whenever it exists. Improper Riemann integrals of this kind cover many cases that arise in applied mathematics and physics.
What Advantages Does the Lebesgue Integral Offer?
The Lebesgue integral partitions the range of a function’s output values rather than its input domain, and this reversal of approach yields several major advantages over the Riemann integral.
The Lebesgue integral can integrate a much larger class of functions than the Riemann integral. It also supports powerful theorems that permit interchanging limits and integrals, including the dominated convergence theorem and the monotone convergence theorem. While the technical setup of Lebesgue theory is more involved than Riemann’s, it pays off through greater generality and cleaner proofs.
Where Does the Lebesgue Integral Fall Short?
Every Riemann-integrable function on a compact interval is Lebesgue integrable, but the reverse relationship breaks down for improper integrals. Some improper Riemann integrals are not Lebesgue integrable under the standard extended definition.
The integral of sin(x)/x from 0 to positive infinity is a clear example of this gap:
[tex]\int_0^{+\infty}\frac{\sin(x)}{x}\,dx[/tex]
This integral is not Lebesgue integrable over [0, ∞) in the absolute sense, yet the improper Riemann integral exists and equals π/2. This shows that the Lebesgue integral, despite being more general in most respects, is in this specific sense weaker than improper Riemann integration.
How Is the Gauge Integral Defined?
The gauge integral resolves the tension between Riemann and Lebesgue integration through a small but consequential change to the Riemann definition. It produces an integral that encompasses the Riemann integral, many improper Riemann integrals, and the full Lebesgue integral.
A standard epsilon-delta definition of the Riemann integral of f: [a,b] → ℝ says that a number L is the integral if, for every ε > 0, there exists a single δ > 0 such that any partition x₀,…,xₙ with sample points a₁,…,aₙ satisfying xᵢ − xᵢ₋₁ < δ for all i gives:
[tex]\left|L – \sum_{i=1}^n f(a_i)(x_i – x_{i-1})\right|<\varepsilon[/tex]
The gauge integral replaces this single uniform δ with a gauge, meaning a positive function δ that can vary across the interval. Formally, L is the gauge integral of f if, for every ε > 0, there exists a function δ: [a,b] → (0, +∞) such that any partition and sample points satisfying:
[tex]x_i – x_{i-1}<\delta(a_i)\quad\text{for all }i,[/tex]
produce the same bound:
[tex]\left|L – \sum_{i=1}^n f(a_i)(x_i – x_{i-1})\right|<\varepsilon.[/tex]
Variants of this definition extend the domain beyond a single closed interval [a,b] in natural ways, though those generalizations go beyond this discussion.
What Are the Key Properties of the Gauge Integral?
A function f is Lebesgue integrable if and only if it is gauge integrable and the gauge integral of |f| is finite. This means Lebesgue integrable functions are precisely the absolutely gauge integrable functions. By analogy with series, the Lebesgue integral corresponds to absolutely convergent series, while the gauge integral corresponds to conditionally convergent series.
Many classical theorems from Riemann and Lebesgue integration hold in the gauge setting, often in cleaner and more general form. The classical fundamental theorem of calculus states that if F is continuous on [a,b] with derivative F′ = f, and f is Riemann integrable, then:
[tex]\int_a^b f(x)\,dx = F(b)-F(a).[/tex]
The requirement that f be Riemann integrable is a real limitation of that classical statement. The gauge integral removes this restriction entirely: if F′ = f everywhere on [a,b] except possibly at countably many points, then f is automatically gauge integrable and:
[tex]\int_a^b f(x)\,dx = F(b)-F(a).[/tex]
Limit theorems, substitution rules, and integration-by-parts formulas also admit stronger and more general versions within the gauge-integral framework than they do under Riemann or Lebesgue integration alone.
Why Isn’t the Gauge Integral Widely Taught?
The gauge integral offers real pedagogical advantages. Its definition is nearly as simple to state as the Riemann integral and becomes intuitive with practice. It unifies the Riemann integral, many improper Riemann integrals, and the Lebesgue integral into a single theory, with the Lebesgue integral recoverable as a special case. Many general theorems also take their cleanest and most general form under the gauge integral.
Despite these strengths, the gauge integral has a significant limitation: it is naturally formulated only for functions from the real numbers to the real numbers. Extensions to ℝⁿ exist, but Lebesgue theory handles general measure spaces and higher-dimensional domains more systematically. Applied scientists usually find the Riemann integral sufficient for their needs, while analysts working in general settings depend on the full Lebesgue theory. These practical considerations help explain why the gauge integral is often left out of standard curricula.
Conclusion
Mathematics tends to value theorems stated in their most beautiful and general form, and the gauge integral is a strong candidate for wider inclusion in undergraduate education on that basis. It is easy to state, it unifies several familiar integrals into one theory, and it produces very general, elegant results.
Frequently Asked Questions
What is the difference between the Riemann integral and the gauge integral?
The Riemann integral uses a single fixed tolerance δ that applies uniformly across the whole interval when checking partitions. The gauge integral replaces this fixed δ with a gauge, a function that can assign a different tolerance to each sample point. This flexibility lets the gauge integral handle a much wider class of functions.
Is every Lebesgue integrable function also gauge integrable?
Yes. A function is Lebesgue integrable if and only if it is gauge integrable and the gauge integral of its absolute value is finite. In other words, Lebesgue integrable functions are exactly the absolutely gauge integrable functions, making the gauge integral a strict generalization in this respect.
Why is sin(x)/x from 0 to infinity important in this discussion?
This integral demonstrates a case where the improper Riemann integral exists and equals π/2, yet the function is not Lebesgue integrable over [0, ∞) in the absolute sense. It illustrates that the Lebesgue integral, despite its generality, does not capture every improper Riemann integral, which is one motivation for the gauge integral.
Does the gauge integral require the derivative to be Riemann integrable in the fundamental theorem of calculus?
No. Under the gauge integral, if F′ = f everywhere on [a,b] except at countably many points, f is automatically gauge integrable and the fundamental theorem of calculus holds. This removes the Riemann integrability requirement present in the classical statement of the theorem.
Why is the gauge integral not commonly taught in university courses?
Its main limitation is that it is naturally defined only for real-valued functions of a real variable, whereas Lebesgue theory extends systematically to general measure spaces and higher dimensions. Since the Riemann integral suffices for most applied work and the Lebesgue integral is essential for advanced analysis, the gauge integral often falls into a curricular gap.
Where can I find a textbook treatment of the gauge integral?
Swartz and DePree’s Introduction to Real Analysis covers it at an introductory level. R. G. Bartle’s A Modern Theory of Integration offers a full, dedicated treatment.
Advanced education and experience with mathematics
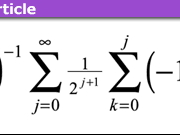
[QUOTE="disregardthat, post: 5561161, member: 49781"]Interesting. So do you as for improper Riemann integrals define for example the gauge integral ##int^{infty}_a f(x) dx## as the limit of the gauge integrals ##lim_{t to infty} int^t_a f(x) dx## (whenever the limit exists or is ##pm infty##) where ##f : [a, infty) to mathbb{R}## is gauge integrable on ##[a,t]## for all ##t geq a##? As far as I can see, you only gave a definition of a gauge integrable function on a closed interval.”You do the exact same thing except (i) replace the reals ##mathbb{R}## with the extended reals and (ii) define the "length" of an unbounded interval (that's the ##x_{i}-x_{i-1}## factor in micromass's definition) as equal to zero. This forces the Riemann sum to be a finite number, and all the proofs can be used unchanged. See Robert McLeod (1980) The Generalized Riemann Integral for an overview.”Assuming the above, what's stopping us from simply defining ##int^{infty}_a f(x) dx## as the limit of the Lebesgue integrals ##lim_{t to infty} int^t_a f(x) dx## (whenever the limit exists or is ##pm infty##) for functions ##f : [a,infty) to infty## which are Lebesgue integrable on ##[a,t]## for all ##t geq a##? Using the same idea for all the different improper integrals would give us a notion of improper Lebesgue integrals, and improperly Lebesgue integrable functions.”There is no such thing as "improper Lebesgue integral" because ##[a,infty)## is a measurable space. ##int_{[a,infty)} f , dmu##, where the right hand side is using the Lebesgue measure, is not improper. Note that ##int_0^infty frac{sin(x)}{x}, dx## is undefined as a Lebesgue integral (it becomes a ##infty-infty## situation), but exists as an improper Riemann integral, or as a gauge integral directly.Remember the reason why we care about Lebesgue at all is because of dominated convergence, but with Riemann we need uniform convergence.
Interesting. So do you as for improper Riemann integrals define for example the gauge integral ##int^{infty}_a f(x) dx## as the limit of the gauge integrals ##lim_{t to infty} int^t_a f(x) dx## (whenever the limit exists or is ##pm infty##) where ##f : [a, infty) to mathbb{R}## is gauge integrable on ##[a,t]## for all ##t geq a##? As far as I can see, you only gave a definition of a gauge integrable function on a closed interval.Assuming the above, what's stopping us from simply defining ##int^{infty}_a f(x) dx## as the limit of the Lebesgue integrals ##lim_{t to infty} int^t_a f(x) dx## (whenever the limit exists or is ##pm infty##) for functions ##f : [a,infty) to infty## which are Lebesgue integrable on ##[a,t]## for all ##t geq a##? Using the same idea for all the different improper integrals would give us a notion of improper Lebesgue integrals, and improperly Lebesgue integrable functions.It seems to me that perhaps the theorem you gave about the equivalence between Lebesgue integrable functions and gauge integrable functions such that ##int |f| < infty## implies that the definition above of a Lebesgue integrable function (proper and improper) is equivalent with the definition of a gauge integrable function.Maybe I'm wrong and missing something here. What exactly can gauge integration do which Lebesgue integration and improper Lebesgue integration like I defined above cannot?Also, what do you do about gauge integrals ##int_A f(x) dx## for arbitrary sets ##A##? For which sets and functions are such integrals defined?
Enlightening! I always thought of Lebesgue as Riemann with running over the null-sets :)
Liked your article too.
minor typo in the first paragraph look for integratal
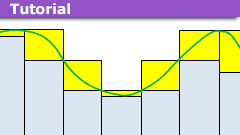
The Insight article has nice pictures that give intuition about the Riemann integral and the Legesgue integral. Is there a useful picture that explains the gauge integral ?The arguments given in favor of the gauge integral focus on the nice implications it provides – if f is gauge integrable then ….. To use such implications in a specific setting, one would need to establish the "f is gauge integrable" clause. I don't get any intuitive understanding of how to do that, except in a trivial case where we can define [itex] delta(x) [/itex] to be a constant function, reverting it to the ordinary [itex] delta [/itex].For example, I gather that [itex] int_0 ^ {infty} frac{sin{x}}{x} [/itex] can be defined as an "extended" gauge integral in the usual way, by taking the limit of a gauge integrals over a finite intervals. So, technically, we need the existence of a different function [itex] delta(x) [/itex] for each of the finite intervals.Does the "gauge" in gauge integral has something to do with the concept of "gauge" in physics? (Unfortunately for me, the concept of a "gauge" in physics isn't very intuitive. There are explanations such ashttps://terrytao.wordpress.com/2008/09/27/what-is-a-gauge/ , but I need someone to explain the explanation!)
[QUOTE="micromass, post: 5527766, member: 205308"]How would "##|f|## is gauge integrable" imply "##f## is measurable"? From my posts follows only that ##|f|## is measurable.”Ok; I see the subtle difference. Thus ''##f## is Lebesgue integrable iff ##f## and ##|f|## are gauge integrable".
How would "##|f|## is gauge integrable" imply "##f## is measurable"? From my posts follows only that ##|f|## is measurable.
[QUOTE="micromass, post: 5527754, member: 205308"]No, that would be incorrect. Can you show why you think your statement is true?”Well if (i) Lebesgue integrable implies measurable and (ii) every gauge integrable function is measurable and (iii) ##f## is Lebesgue integrable iff ##f## is measurable and ##|f|## is gauge integrable" (three assertions taken from your posts) then my statement follows.
[QUOTE="A. Neumaier, post: 5527731, member: 293806"]Then the optimal statement should be ''##|f|## is gauge integrable iff ##f## is Lebesgue integrable'', shouldn't it?”No, that would be incorrect. Can you show why you think your statement is true?
[QUOTE="micromass, post: 5527720, member: 205308"]No, every gauge integrable function is measurable.”Then the optimal statement should be ''##|f|## is gauge integrable iff ##f## is Lebesgue integrable'', shouldn't it?
[QUOTE="A. Neumaier, post: 5527719, member: 293806"]OK, thanks. Are there nonmeasurable functions ##f## for which both ##f## and ##|f|## are gauge integrable? (assuming ZFC)”No, every gauge integrable function is measurable.
[QUOTE="micromass, post: 5527718, member: 205308"]Lebesgue integrable implies measurable, so I don't know why you put in a condition "measurable and Lebesgue integrable".” OK, thanks. Are there nonmeasurable functions ##f## for which both ##f## and ##|f|## are gauge integrable? (assuming ZFC)
[QUOTE="A. Neumaier, post: 5527717, member: 293806"]The two answers don't quite match. It seems to me that you wanted to say that ''##|f|## is gauge integrable iff ##f## is measurable and Lebesgue integrable''. Is this the correct assertion?”Lebesgue integrable implies measurable, so I don't know why you put in a condition "measurable and Lebesgue integrable". So no, it is not the correct assertion. It is "##f## is Lebesgue integrable iff ##f## is measurable and ##|f|## is gauge integrable".
[QUOTE="micromass, post: 5527686, member: 205308"]Read the rest of the post for the exact statement that is true. It also says that the statement as posted is false.Yes.”The two answers don't quite match. It seems to me that you wanted to say that ''##|f|## is gauge integrable iff ##f## is measurable and Lebesgue integrable''. Is this the correct assertion?
[QUOTE="A. Neumaier, post: 5527684, member: 293806"]What do you mean by ''essentially correct"? The question was a precise mathematical statement, so it is either known to be true or not known to be true.”Read the rest of the post for the exact statement that is true. It also says that the statement as posted is false.”And is the inverse also true, is every Lebesgue integrable function also gauge integrable?”Yes.
[QUOTE="micromass, post: 5527671, member: 205308"]That is essentially correct. We just want ##f## to be measurable/gauge integrable to exclude pathological cases having to do with nonmeasurable functions.”What do you mean by ''essentially correct"? The question was a precise mathematical statement, so it is either known to be true or not known to be true. And is the inverse also true, is every Lebesgue integrable function also gauge integrable?
[QUOTE="wrobel, post: 5527653, member: 593228"]Thanks.So if ##|f|## is gauge integrable then ##f## it is Lebesgue integrable?”That is essentially correct. We just want ##f## to be measurable/gauge integrable to exlcude pathological cases having to do with nonmeasurable functions.
Thanks.So if ##|f|## is gauge integrable then ##f## it is Lebesgue integrable?
[QUOTE="wrobel, post: 5527588, member: 593228"]Does the gauge integral allow to define spaces analogous to ##L^p##?”The situation is the same as with convergent and absolutely convergent series. Absolutely convergent series allow us to define ##ell^p##. Convergent series is general do not. In the same way, the absolutely convergent integrals can be used to define ##L^p##. Note that ##|f|## is absolutely convergent iff ##f## is Lebesgue integral.”If the gauge integral ##int|f|=0## then what can we say about ##f##?”We can say that ##f=0## a.e. just as with the Lebesgue integral.
Does the gauge integral allow to define spaces analogous to ##L^p##? If the gauge integral ##int|f|=0## then what can we say about ##f##?
Here is the theorem of differentiation under the integral sign for the gauge integral:Theorem: Let ##f:[a,b]times [c,d]rightarow mathbb{R}## (where ##b## can be infinity) such that for each ##tin [c,d]##, the function ##xrightarrow f(x,t)## is measurable on ##[a,b]##.Suppose that:1) There exists ##tin [c,d]## such ##xrightarrow f(x,t)## is gauge integrable.2) The partial derivative ##frac{partial f}{partial t}## exists on ##[a,b]times [c,d]##.3) There are gauge integrable functions ##alpha## and ##omega## such that[tex]alpha(x)leq frac{partial f}{partial t}(x,t)leq omega(x)[/tex]for all ##xin [c,d]## and ##tin [a,b]##.1) Then ##xrightarrow f(x,t)## is gauge integrable for each ##tin [c,d]##.2) The function ##xrightarrow frac{partial f}{partial t}## is guage integrable for each ##tin [c,d]##3) We have[tex]frac{d}{dt}int_a^b f(x,t)dx = int_a^b frac{partial f}{partial t}dx[/tex]In particular, if ##f(x,t) = e^{-tx}frac{sin(x)}{x}##, then this is clearly measurable in ##x## since it is continuous.Setting ##t=1## gives us ##e^{-x}frac{sin(x)}{x}## which is gauge integrable by the following theorem.Theorem: A measurable function ##g## is gauge integrable iff there are gauge integrable functions ##g_1##, ##g_2## such that ##g_1leq gleq g_2##.We have ##frac{partial f}{partial t} = -e^{-tx}sin(x)## exists on ##[0,+infty]times [varepsilon,1]## and is easily seen to be gauge integrable by using the above Theorem. So the theorem applies, at least for ##tin [varepsilon, 1]##. So for those ##t##, we can indeed et[tex]int_0^{+infty} e^{-tx}frac{sin(x)}{x}dx = frac{pi}{2} – text{arctan}(t)[/tex]Then we would need to switch limit and integral to conclude that ##int_0^{+infty}frac{sin(x)}{x}dx = frac{pi}{2}##. This is provided in the document I linked.
[QUOTE="A. Neumaier, post: 5527436, member: 293806"]The main reason why the standard courses about integration treat the Lebesgue integral rather than the Henstock integral is that the former has much stronger properties required in all applications to measure theory and functional analysis.One cannot do most of modern mathematics without the Lebesgue integral, while one can do most of it without the Henstock integral. Being maximally general is simply something very different from being maximally useful.”Almost all of the theorems of Lebesgue integration also hold for the gauge integral. This includes stuff like dominated convergence and integration under the integral sign.[QUOTE="A. Neumaier, post: 5527437, member: 293806"]The justification must be based on proven properties of the integral. Are these properties satisfied for the Lebesgue integral? For the Henstock integral?”Yes, they are.[QUOTE="strangerep, post: 5527446, member: 70760"]Oh, ok. (I knew about DUI already, of course, but hadn't seen it applied to sin(x)/x.) In any case, I now realize I misinterpreted your article. I was replying to your statement:but forgot that you had said earlier that it's Riemann-integrable.DUI tends to be used quite freely in theoretical physics, so it would be useful to know if there's any easy ways to tell where it doesn't work. Perhaps a subject for another insights article? :oldbiggrin:”That's a good idea!
[QUOTE="A. Neumaier, post: 5527437, member: 293806"]This is a heuristic recipe that requires justification. Why is one allowed to do that in this particular case? Surely there are conditions on the integrand needed to make it work as it is known yhat the trick may fail to give the correct answer.The justification must be based on proven properties of the integral. Are these properties satisfied for the Lebesgue integral? For the Henstock integral?”From Necessary and Sufficient Conditions for Differentiating Under the Integral Sign by Erik TalvilaTheorem Let ##f:[alpha,beta] times [a,b] to mathbb{R}##. Suppose that ##f(cdot, y)## is ##ACG_*## on ##[alpha, beta]## for almost all ##y in (a,b)##. Then ##F:= int_a^b f(cdot,y) , dy## is ##ACG_*## on ##[alpha,beta]## and ##F'(x) = int_a^b f_1(x,y) , dy## for almost all ##x in (alpha,beta)## if and only if##int_{x=s}^{t} int_{y=a}^b f_1 (x,y) dy dx = int_{y=a}^{b} int_{x=s}^t f_1(x,y) dx dy## for all ##[s,t]subset [alpha,beta]##.Recall, a function is said to be absolutely continuous in the restricted sense on ##Esubset [a,b]## (##AC_*##) if for all ##epsilon > 0## there exists ##delta > 0## such that ##Sigma_{i=1}^{N} sup_{x,y in [x_i, y_i]} | F(x) – F(y)| < epsilon## for all finite sets of disjoint open intervals with endpoints in E and ##Sigma_{i=1}^N (y_i-x_i) < delta##.A function is said to be generalised absolutely continuous in the restricted sense on E (##ACG_*##) if it is continuous and E is a countable union of sets on which it is ##AC_*##
[QUOTE="A. Neumaier, post: 5527437, member: 293806"]This is a heuristic recipe that requires justification. Why is one allowed to do that in this particular case? Surely there are conditions on the integrand needed to make it work as it is known yhat the trick may fail to give the correct answer.The justification must be based on proven properties of the integral. Are these properties satisfied for the Lebesgue integral? For the Henstock integral?”From Necessary and Sufficient Conditions for Differentiating Under the Integral Sign by Erik TalvilaTheorem Let ##f:[alpha,beta] times [a,b] to mathbb{R}##. Suppose that ##f(cdot, y)## is ##ACG_*## on ##[alpha, beta]## for almost all ##y in (a,b)##. Then ##F:= int_a^b f(cdot,y) , dy## is ##ACG_*## on ##[alpha,beta]## and ##F'(x) = int_a^b f_1(x,y) , dy## for almost all ##x in (alpha,beta)## if and only if##int_{x=s}^{t} int_{y=a}^b f_1 (x,y) dy dx = int_{y=a}^{b} int_{x=s}^t f_1(x,y) dx dy## for all ##[s,t]subset [alpha,beta]##.Recall, a function is said to be absolutely continuous in the restricted sense on ##Esubset [a,b]## (##AC_*##) if for all ##epsilon > 0## there exists ##delta > 0## such that ##Sigma_{i=1}^{N} sup_{x,y in [x_i, y_i]} | F(x) – F(y)| < epsilon## for all finite sets of disjoint open intervals with endpoints in E and ##Sigma_{i=1}^N (y_i-x_i) < delta##.A function is said to be generalised absolutely continuous in the restricted sense on E (##ACG_*##) if it is continuous and E is a countable union of sets on which it is ##AC_*##
[QUOTE="micromass, post: 5526994, member: 205308"]One approach is to differentiate under the integral sign. […][/quote] Oh, ok. (I knew about DUI already, of course, but hadn't seen it applied to sin(x)/x.) In any case, I now realize I misinterpreted your article. I was replying to your statement:[quote=micromass]Furthermore, integrals like ##int_0^infty sin(x)/x ; dx## that can not be found by Lebesgue, can be found by the gauge integral and yield sensible answers[/quote]but forgot that you had said earlier that it's Riemann-integrable.DUI tends to be used quite freely in theoretical physics, so it would be useful to know if there's any easy ways to tell where it doesn't work. Perhaps a subject for another insights article? :oldbiggrin:
[QUOTE="micromass, post: 5526994, member: 205308"]to differentiate under the integral sign”This is a heuristic recipe that requires justification. Why is one allowed to do that? The justification must be based on proven properties of the integral. Are these properties satisfied for the Lebesgue integral? For the Henstock integral?
The main reason why the standard courses about integration treat the Lebesgue integral rather than the Henstock integral is that the former has much stronger properties required in all applications to measure theory. One cannot do most of modern mathematics without the Lebesgue integral, while one can do most of it without the Henstock integral. being maximally general is simply something very different from being maximally useful.
[QUOTE="strangerep, post: 5526850, member: 70760"][USER=205308]@micromass[/USER]: Coincidentally, I recently read a bit about the "Henstock–Kurzweil" integral, which I understand is the same thing as the Gauge Integral? (Btw, is there any reason you didn't mention that name?)”Yes, it is the same thing. I'll add the various names to the article. Thanks”Regarding the integral $$int_0^infty frac{sin(x)}{x}, dx ~~,$$I've only ever seen that performed by contour integration (i.e., interpreted as a Cauchy PV integral). How is it done by Gauge Integration? (Maybe you could post an online link to the details?)”One approach is to differentiate under the integral sign. Consider ##F(t) = int_0^{+infty} e^{-tx}frac{sin(x)}{x}dx##. Then [tex]F'(t) = -int_0^{+infty} e^{-tx} sin(x)dx = -frac{1}{1+t^2}[/tex]So ##F(t) = frac{pi}{2} – text{arctan}(t)##. Letting ##trightarrow 0## gives us the value of ##pi/2##.Here you can find more details: http://www.math.uconn.edu/~kconrad/blurbs/analysis/diffunderint.pdf This document doesn't deal with the gauge integral, but everything in the document applies to that setting as well.”And speaking of contour integration, one thing I like about Cauchy PV integrals is their relationship to Lebesgue integrals. But I get the impression from your article that one cannot in general achieve such a close relationship with Gauge Integrals, since the domain is ##mathbb C##, not ##mathbb{R}## ?”Right. It is possible though to define the gauge integral on ##mathbb{C}##, but this is technical. In any case, it's not something I've looked into.
[USER=205308]@micromass[/USER]: Coincidentally, I recently read a bit about the "Henstock–Kurzweil" integral, which I understand is the same thing as the Gauge Integral? (Btw, is there any reason you didn't mention that name?)Regarding the integral $$int_0^infty frac{sin(x)}{x}, dx ~~,$$I've only ever seen that performed by contour integration. How is done by Gauge Integration? (Maybe you could post an online link to the details?)And speaking of contour integration, one thing I like about Cauchy PV integrals is their relationship to Lebesgue integrals. But I get the impression from your article that one cannot in general achieve such a close relationship with Gauge Integrals, since the domain is ##mathbb C##, not ##mathbb{R}## ?
Enlightening! I always thought of Lebesgue as Riemann with running over the null-sets. This article cleared this wrong view.