Questions on dynamics - Newton's laws of motion

[fterh]

1. A chain of mass M and length L is suspended vertically with its lower end touching a scale. The chain is released and falls onto the scale. What is the reading of the scale when a length of the chain x has fallen? You may neglect the size of the individual links.

2. A smooth wedge, whose central cross-section is a triangle ABC, right-angled at C, rests with the face containing AB on a smooth horizontal plane. When the wedge is held fixed, a particle released from rest, takes a time t1 to slide the full length of CA. The corresponding time for CB is t2. Show that tan A = t2/t1, and find AB in terms of t1 and t2. If the mass of the wedge is n times that of the particle and the wedge is free to move, show that the time of sliding down CA becomes:

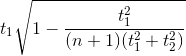
3. A light inextensible string passes round a fixed smooth pulley and carries at each end a smooth pulley of mass 1.0 kg. Over each of these pulleys a string hangs, one carrying masses of 1.0 kg and 2.0 kg at its ends, the other masses of 1.0 kg and 3.0 kg. The system is set in motion. Find the acceleration of the pulleys and the tension in the string to which they are attached.

----------

1. For the first question, I am guessing that in addition to the weight of the portion of the chain lying on the scale, the momentum of the movement of the chain has to be taken into account?

So the weight of the portion would be Mgx/L, while the momentum would be Mx/L*v. v (velocity) = g*t = gx/0.5v. Thus p = Mx/L * gx/0.5v = Mgx^2/0.5Lv.

The answer should be: 3Mgx/L.

2. I got the "Show that tan A = t2/t1" part, and I found AB using pythagoras theorem. However I'm not too sure how to solve for the "free moving wedge" part. I'm guessing that I'd have to calculate the horizontal component of the normal force, to determine the rate of acceleration of the wedge away from the particle. Then I got stuck. Heh.

3. I thought I had it, this is my workings.

http://i.imgur.com/CtSp3.jpg

The answer is: 0.426ms^(-2), 37.5N. My tension is wrong, so I didn't bother calculating for acceleration. I thought my methodology was correct, apparently not. Hmm.

 

[omoplata]

For question 1, to find the force due to the change of momentum, I tried finding the change of momentum of an infinitesimally small length of the chain, and got $\frac{3 M g x}{2 L}$ for the final answer.

 

[fterh]

For question 1, to find the force due to the change of momentum, I tried finding the change of momentum of an infinitesimally small length of the chain, and got $\frac{3 M g x}{2 L}$ for the final answer.

So for question 1, do you have to add the force due to the change of momentum to the weight of the amount of chain already lying on the scale?

And since neither m nor v is a constant, do you use F = ma or F = v(dm/dt)? (Sorry, I'm still a newb! :()

 

[omoplata]

So for question 1, do you have to add the force due to the change of momentum to the weight of the amount of chain already lying on the scale?

That's what I did.

And since neither m nor v is a constant, do you use F = ma or F = v(dm/dt)?

I considered the very small mass whose velocity is changed as the chain drops a distance $\delta x$, and applied $F=\frac{d p}{d t}$ where $p$ is the momentum.

But I don't get the answer they've stated. I get $\frac{3 M g x}{2 L}$ instead of $\frac{3 M g x}{L}$.

 

[fterh]

That's what I did.

I considered the very small mass whose velocity is changed as the chain drops a distance $\delta x$, and applied $F=\frac{d p}{d t}$ where $p$ is the momentum.

But I don't get the answer they've stated. I get $\frac{3 M g x}{2 L}$ instead of $\frac{3 M g x}{L}$.

So since you're considering an infinitesimally small mass and its change in velocity, so mass is constant in your calculation?

And I found an identical problem and its solution here (https://www.physicsforums.com/showthread.php?t=93553). Since you're interested in learning more, you may want to look at it! :D

Edit: I found this document (http://bit.ly/m0ezB0) that says that "Since the mass of the chain on the surface increases as the
chain falls, we need to consider this a variable mass system." But I can argue that the velocity increases as the chain falls too, so we could also consider it a fixed mass, variable velocity system? Can anybody shed some light?

 

[omoplata]

Oh, I got $\frac{3 M g x}{L}$. It was just an algebra mistake . I divided by 2 instead of multiplying.

My reasoning is the same as Doc Al's in that other tread. Except that he directly finds the rate of change of momentum by differentiating the total stationary mass of the chain, I took an infinitesimal time interval $\delta t$ and put $\lim \delta t \rightarrow 0$ to find $\frac{d p}{d t}$.

 

[omoplata]

I looked at the document you linked to. But I don't know what the argument against $\frac{d v}{d t}$ being considered is. But when I did differentiation in first principles, I did not encounter this problem. At least, not as far as I can tell.

OK, since you have found enough solutions, I'll post mine too, so you can compare.

Consider an infinitesimal time $\delta t$. The chain travels distance $\delta x$ during this time.

Consider the mass element $\delta m$ hitting the scale during this time.

$$\delta m = \frac{M}{L} \delta x$$

The infinitesimal momentum of the mass element, when downwards is considered to be the positive direction, is $\delta p = \delta m v$, where $v$ is the velocity.

The change of momentum downwards is $\Delta p = 0 - \delta p = - \delta p$. But since we are interested in finding the reaction force on the scale, which is the rate of change of momentum upwards, we should consider the rate of change of momentum upwards, which is $- \Delta p = \delta p$.

The extra reaction force on the scale, i.e. rate of change of momentum upwards is,

$$\frac{\delta p}{\delta t} = \frac{M v}{L} \frac{\delta x}{\delta t}$$

Applying limits,

$$F = \lim_{\delta t \rightarrow 0} - \frac{\Delta p}{\delta t} = \frac{M v}{L} \lim_{\delta t \rightarrow 0} \frac{\delta x}{\delta t} = \frac{M v}{L} \frac{d x}{d t} = \frac{M v^{2}}{L}$$

But since $v^{2} = 2 g x$,

$$F = \frac{2 M g x}{L}$$

 

[fterh]

I looked at the document you linked to. But I don't know what the argument against $\frac{d v}{d t}$ being considered is. But when I did differentiation in first principles, I did not encounter this problem. At least, not as far as I can tell.

OK, since you have found enough solutions, I'll post mine too, so you can compare.

Consider an infinitesimal time $\delta t$. The chain travels distance $\delta x$ during this time.

Consider the mass element $\delta m$ hitting the scale during this time.

$$\delta m = \frac{M}{L} \delta x$$

The infinitesimal momentum of the mass element, when downwards is considered to be the positive direction, is $\delta p = \delta m v$, where $v$ is the velocity.

The change of momentum downwards is $\Delta p = 0 - \delta p = - \delta p$. But since we are interested in finding the reaction force on the scale, which is the rate of change of momentum upwards, we should consider the rate of change of momentum upwards, which is $- \Delta p = \delta p$.

The extra reaction force on the scale, i.e. rate of change of momentum upwards is,

$$\frac{\delta p}{\delta t} = \frac{M v}{L} \frac{\delta x}{\delta t}$$

Applying limits,

$$F = \lim_{\delta t \rightarrow 0} - \frac{\Delta p}{\delta t} = \frac{M v}{L} \lim_{\delta t \rightarrow 0} \frac{\delta x}{\delta t} = \frac{M v}{L} \frac{d x}{d t} = \frac{M v^{2}}{L}$$

But since $v^{2} = 2 g x$,

$$F = \frac{2 M g x}{L}$$

My argument, simply put, is challenging the assumption that v is a constant for an infinitesimal period of time. Why make v a constant, and dx/dt, rather than make x a constant, and dv/dt? :X

 

[omoplata]

Why make v a constant, and dx/dt, rather than make x a constant, and dv/dt? :X

I don't really understand this question. But I didn't consider either $v$ or $x$ to be a constant.

How would you do it?

 

[fterh]

I don't really understand this question. But I didn't consider either $v$ or $x$ to be a constant.

How would you do it?

Because in your workings,

So in this case isn't v like a constant, since there is no delta or d in front of it?

 

[omoplata]

I see what you mean. The $v$ I used is for the velocity of the part of the chain hitting the scale at time $t$. At time $t + \delta t$ it's 0. I don't know if that makes $v$ a constant.

 

[fterh]

I see what you mean. The $v$ I used is for the velocity of the part of the chain hitting the scale at time $t$. At time $t + \delta t$ it's 0. I don't know if that makes $v$ a constant.

Ok I'll think about it. Meanwhile could you help me look at q3? :X I'm so close to that one, yet I just couldn't get the answer. :(

 

[omoplata]

The way you've done it, the 2kg mass has an acceleration of 2a downwards and the 1kg mass connected to it has an of 1a upwards. Yet these two masses are at the ends of the same string. So the length of the string will change. This is not right. The length of the string must be constant. The same thing goes for the 3kg mass on the right.

The accelerations of all the pulleys and the masses are connected by the conditions that the strings connecting them are of constant length. You must use this to find all the accelerations in terms of just one unknown. Then apply Newton's 2nd law.

 

[omoplata]

You must use this to find all the accelerations in terms of just one unknown.

Sorry, mistake. You can't reduce them to just one unknown term. But you can reduce the number of unknowns. Use the condition that the three strings are constant. There are 6 objects. So you'll get (6-3) = 3 unknown terms for the accelerations.

 

[fterh]

The way you've done it, the 2kg mass has an acceleration of 2a downwards and the 1kg mass connected to it has an of 1a upwards. Yet these two masses are at the ends of the same string. So the length of the string will change. This is not right. The length of the string must be constant. The same thing goes for the 3kg mass on the right.

The accelerations of all the pulleys and the masses are connected by the conditions that the strings connecting them are of constant length. You must use this to find all the accelerations in terms of just one unknown. Then apply Newton's 2nd law.

uh, but isn't 2a and a referring to the forces (given by mass * acceleration)?

 

[omoplata]

Oh, OK.

But that would only be valid if the pulleys are stationary. You have to take their accelerations into account when applying Newton's 2nd law.

 

[fterh]

Oh, OK.

But that would only be valid if the pulleys are stationary. You have to take their accelerations into account when applying Newton's 2nd law.

Because I remember my teacher going through a similar (albeit much simpler) question, and this is the method she employed.

In this case, I am applying F = ma. The resultant forces acting on the masses are different (given by mg-T and T-mg for the heavier and lighter one respectively), but acceleration is the same. So I solve for T, which is the force acting on the pulley.

Is my application of Newton's 2nd Law fundamentally incorrect? :X

 

[omoplata]

Let's suppose there is an upward acceleration of $a_{2}$ on the ikg pulley attached to the 2kg and 1kg masses. And suppose the acceleration on the 2kg mass relative to the pulley is $a_{1}$ downwards. Then the acceleration relative to the ground is $a_{1} - a_{2}$ downwards for the 2kg mass and $a_{1} + a_{2}$ upwards for the 1kg mass. If you are applying F = ma for the inertial reference frame of the earth, you have to use these accelerations.

 

[fterh]

Let's suppose there is an upward acceleration of $a_{2}$ on the ikg pulley attached to the 2kg and 1kg masses. And suppose the acceleration on the 2kg mass relative to the pulley is $a_{1}$ downwards. Then the acceleration relative to the ground is $a_{1} - a_{2}$ downwards for the 2kg mass and $a_{1} + a_{2}$ upwards for the 1kg mass. If you are applying F = ma for the inertial reference frame of the earth, you have to use these accelerations.

I get what you mean. But shouldn't you be able to disregard the upward acceleration of the pulley, since if you consider the masses as a "close system", the acceleration of the "entire system" shouldn't affect the acceleration of the objects within the system?

 

[omoplata]

But shouldn't you be able to disregard the upward acceleration of the pulley, since if you consider the masses as a "close system", the acceleration of the "entire system" shouldn't affect the acceleration of the objects within the system?

I think the correct way of solving this is to consider the acceleration of the entire system as well.

The best way to see is to solve it and see whether you get the given answer.

 

[fterh]

I think the correct way of solving this is to consider the acceleration of the entire system as well.

The best way to see is to solve it and see whether you get the given answer.

In this case, when forming equations, I cannot take the mass of the heavier pulley to be 1+1+3=5kg, can I? Since the apparent mass of the pulley will seem to have "decreased", because of the motion of the masses.

 

[omoplata]

I cannot take the mass of the heavier pulley to be 1+1+3=5kg, can I? Since the apparent mass of the pulley will seem to have "decreased", because of the motion of the masses.

The way I do it is apply F = ma to each of the masses and pulleys separately. The mass of the pulley is 1kg. If the tension of the lower string is $T_{1}$ and the tension in the upper string is $T_{2}$, you have a net force $T_{2} - 2 T_{1}$ acting upwards.

 

[fterh]

I tried considering the acceleration of the system (defined to be the 2kg and 1kg mass), so I have an a1 (acceleration of the system) as well as a2 (acceleration of the masses).

Eventually I got a 0=0 equation. Heh. I'm confused. Have you tried? Can you get the answer? :/

 

[omoplata]

I'll name the tension on the stationary pulley $T$ and it's acceleration so that the 1kg pulley on the right comes down as $a$. Name the tension of the string on the left 1kg pulley $T_{1}$ and its acceleration RELATIVE TO THE PULLEY so that the 2kg mass comes down $a_{1}$. Name the tension of the string on the right 1kg pulley $T_{2}$ and its acceleration RELATIVE TO THE PULLEY so that the 3kg mass comes down $a_{2}$. Name the masses from left to right $m_1$ (1kg), $m_2$ (2kg), $m_3$ (1kg) and $m_4$ (3kg). Name the mass of the left 1kg pulley $m_5$ and the right 1kg pulley $m_6$.

Applying Newton's 2nd law to the 6 masses,
$$T - 2 T_1 - m_5 g = m_5 a$$
$$T_1 - m_1 g = m_1 (a_1 + a)$$
$$m_2 g - T_1 = m_2 (a_1 - a)$$
$$2 T_2 - T + m_6 g = m_6 a$$
$$T_2 - m_3 g = m_3 (a_2 - a)$$
$$m_4 g - T_2 = m_4 (a_2 + a)$$

There are 6 unknowns $(T, T_1, T_2, a, a_1, a_2)$ and 6 linear equations. You should be able to solve it for $T$ and then find $a$ or vice versa.

PS. I didn't actually try to solve them because I'm lazy. So check that the equations are correct first. If they are correct and if you have trouble solving them, I'll help you.