- #1
fog37
- 1,568
- 108
- TL;DR Summary
- Trying to understand why a random variables assigns a unique value only to elementary events and not to composite events
Hello,
A sample space is the set of all possible elementary events. A random "variable" is really a real-valued function that associates a single real number to every elementary events. For example, in the case of a fair die, the sample space is ##\Omega={1,2,3,4,5,6}##. Each number is an elementary event.
A composite event would be, for example, the outcome being larger than 3: composite event {4,5,6}. Couldn't a random variable also apply to composite events like this? Or does it only assign numbers to elementary events?
When we launch two fair dies, the space of the events is
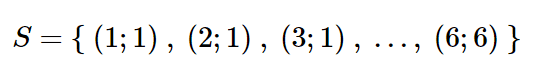
In this case, each pair is an elementary event and the numbers represent the number on the face of each die. A random variable could be defined in different ways, for example X could be the sum of the numbers on the two faces. Or the product, etc.
The sum of two numbers or their product, etc. are not elementary events in themselves but a concept applied to the elementary event. The elementary event is (1;1). The random variable is "their sum", "their product", etc., correct?
Thank you!
A sample space is the set of all possible elementary events. A random "variable" is really a real-valued function that associates a single real number to every elementary events. For example, in the case of a fair die, the sample space is ##\Omega={1,2,3,4,5,6}##. Each number is an elementary event.
A composite event would be, for example, the outcome being larger than 3: composite event {4,5,6}. Couldn't a random variable also apply to composite events like this? Or does it only assign numbers to elementary events?
When we launch two fair dies, the space of the events is
In this case, each pair is an elementary event and the numbers represent the number on the face of each die. A random variable could be defined in different ways, for example X could be the sum of the numbers on the two faces. Or the product, etc.
The sum of two numbers or their product, etc. are not elementary events in themselves but a concept applied to the elementary event. The elementary event is (1;1). The random variable is "their sum", "their product", etc., correct?
Thank you!