- #1
bobinthebox
- 29
- 0
- TL;DR Summary
- Given an elastic block, describe a possible set of boundary conditions so that the block can slight on a plane parallel to ##e_1 e_3## direction
[Mentor Note -- Thread moved to the ME forum to get better views]
Let's consider an incompressible block of Neo-Hookean material. Let the initial reference geometry be described by ##B=[0,b] \times [0,b] \times [0,h]##. The professor gave me the following task:
I came up with the following B.Cs. Here ##u(p) = x(p)-p## is the displacement corresponding to a deformation map #x#
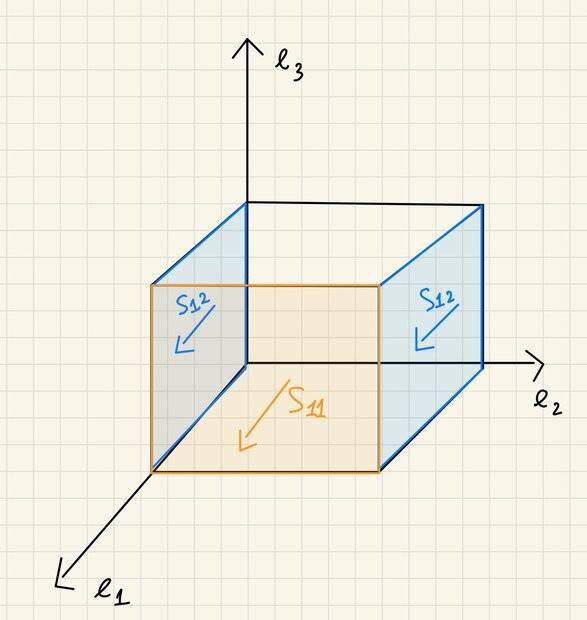 Do you think that the problem is set up in the proper way? I am afraid that I loose the incompressibility in this way
Do you think that the problem is set up in the proper way? I am afraid that I loose the incompressibility in this way
Let's consider an incompressible block of Neo-Hookean material. Let the initial reference geometry be described by ##B=[0,b] \times [0,b] \times [0,h]##. The professor gave me the following task:
Of course there can be many possibilities. I was thinking to the case when the block is extended in the ##e_1## direction by a load factor of #\delta#.Set up the boundary conditions of your problem so that the lateral surfaces can move on a plane parallel to the ##e_1 e_3## plane. Since you have to work in the reference, use first Piola-Kirchoff stress tensor ##S##.
I came up with the following B.Cs. Here ##u(p) = x(p)-p## is the displacement corresponding to a deformation map #x#
- ##S_{22}=0## so that I have no normal stress in the lateral faces with normal ##e_2##.
- ##e_3 \cdot S(-e_1) = e_2 \cdot S(e_1)=0## so that I am constraining the block to do not move
- ##e_2 \cdot S(e_1) = e_3 \cdot S(e_1)=0## same as above, but on the the face with normal ##e_1##
- ##u_1(p)=\delta## for ##p \in \text{bottom face}## i.e. displacement equal to ##\delta## in the ##e_1## direction##.
Last edited by a moderator: