Solve the problem involving the cubic function

[chwala]

Homework Statement

See attached

Relevant Equations

cubic equations and roots.

The problem and solution are posted... no. 8

I may need insight on common difference ...

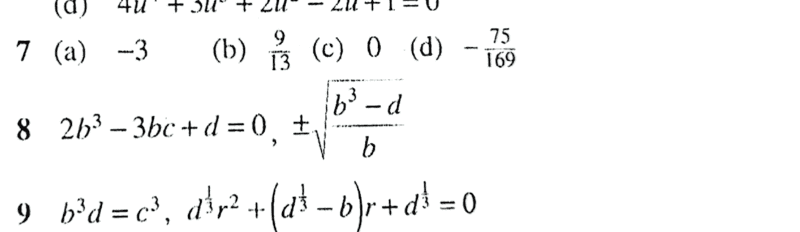
In my lines i have,
Let the roots be $(b), (b-1)$ and $(b+1)$.
Then,
$x^3-3bx^2+3cx-d = a(x-b(x-b+1)(x-b-1)$

$x^3-3bx^2+3cx-d= a(x^3-3bx^2+3b^2x-x-b^3+b)$
$a=1$.

Let

$f(x)=x^3-3bx^2+3b^2x-x-b^3+b$

Using Factor theorem,

$f(b)=b^3-3b^3+3b^3-b-b^3+b=0$

$f(b)=0$ thus $b$ is a root of the cubic equation.

For the condition, we solve the equations,

$x^3-3bx^2+3cx-d= x^3-3bx^2+3b^2x-x-b^3+b$

$(3b^2-1)=3c$
$-b^3+b=-d$

$⇒b(b^2-(3b^2-3c))=d$

$b(-2b^2+3c)=d$

$2b^3-3bc+d=0$.

Any insight ...let me work on common difference later...

 

[pasmith]

You are asked to prove that $b$ is a root; you cannot therefore assume that $b$ is a root, or that the common difference is 1.

The cubic with leading cofficient 1 with $p$ and $p \pm q$ as roots is $$(x - p)((x - p)^2 - q^2) \equiv (x - p)^3 - q^2(x-p).$$ To compare this to our cubic, complete the cube to obtain $$\begin{split} x^3 - 3bx^2 + 3cx - d &= (x - b)^3 - 3(b^2 - c)x + b^3 - d \\ &= (x - b)^3 - 3(b^2 - c) \left(x - \frac{b^3 - d}{3(b^2 - c)}\right). \end{split}$$ Now by comparison we must have $$\begin{split} p &= b = \frac{b^3 - d}{3(b^2 - c)} \\ q^2 &= 3(b^2 - c).\end{split}$$

 

[chwala]

You are asked to prove that $b$ is a root; you cannot therefore assume that $b$ is a root, or that the common difference is 1.

The cubic with leading cofficient 1 with $p$ and $p \pm q$ as roots is $$(x - p)((x - p)^2 - q^2) \equiv (x - p)^3 - q^2(x-p).$$ To compare this to our cubic, complete the cube to obtain $$\begin{split} x^3 - 3bx^2 + 3cx - d &= (x - b)^3 - 3(b^2 - c)x + b^3 - d \\ &= (x - b)^3 - 3(b^2 - c) \left(x - \frac{b^3 - d}{3(b^2 - c)}\right). \end{split}$$ Now by comparison we must have $$\begin{split} p &= b = \frac{b^3 - d}{3(b^2 - c)} \\ q^2 &= 3(b^2 - c).\end{split}$$

I will go through your steps...cheers.

 

[WWGD]

In order to show $b$ is a root, you need to show $f(b)=0$. Notice that the only thing you can conclude from the assumption of arithmetic progression is that the roots are $b-r,b, b+r$, or $b, b+r, b+2r$. You're assuming $r=1$.

 

[chwala]

In order to show $b$ is a root, you need to show $f(b)=0$. Notice that the only thing you can conclude from the assumption of arithmetic progression is that the roots are $b-r,b, b+r$, or $b, b+r, b+2r$. You're assuming $r=1$.

yes, that was a mistake. I will re look into the steps...

 

[SammyS]

In order to show $b$ is a root, you need to show $f(b)=0$. Notice that the only thing you can conclude from the assumption of arithmetic progression is that the roots are $b-r,b, b+r$, or $b, b+r, b+2r$. You're assuming $r=1$.

While this did bear repeating, @pasmith covered this all very well in his earlier post.

 

[chwala]

While this did bear repeating, @pasmith covered this all very well in his earlier post.

I think the emphasis on the $r$ part ... specifically let me state it as ${d}$ in terms of arithmetic progression was necessary...

 

[chwala]

You are asked to prove that $b$ is a root; you cannot therefore assume that $b$ is a root, or that the common difference is 1.

The cubic with leading cofficient 1 with $p$ and $p \pm q$ as roots is $$(x - p)((x - p)^2 - q^2) \equiv (x - p)^3 - q^2(x-p).$$ To compare this to our cubic, complete the cube to obtain $$\begin{split} x^3 - 3bx^2 + 3cx - d &= (x - b)^3 - 3(b^2 - c)x + b^3 - d \\ &= (x - b)^3 - 3(b^2 - c) \left(x - \frac{b^3 - d}{3(b^2 - c)}\right). \end{split}$$ Now by comparison we must have $$\begin{split} p &= b = \frac{b^3 - d}{3(b^2 - c)} \\ q^2 &= 3(b^2 - c).\end{split}$$

Your steps are clear; though on the last line where you have,

$p=b=\dfrac{b^3-d}{3(b^2-c)}$ is a bit confusing, this would imply that

$b=\dfrac{b^3-d}{3(b^2-c)}$ which may not be true ... unless we have the condition that

$2b^3=3bc+d$.

 

[chwala]

In order to show $b$ is a root, you need to show $f(b)=0$. Notice that the only thing you can conclude from the assumption of arithmetic progression is that the roots are $b-r,b, b+r$, or $b, b+r, b+2r$. You're assuming $r=1$.

Okay using what you and @pasmith hinted,
let the roots be $(b-r), b$ and $(b+r)$
then we shall have $(x-b)(x-b-r)9x-b+r)=(x-b)[(x-b)^2 -r^2]$

then,

$(x-b)^3-r^2(x-b)=x^3-3x^2b +3b^2x-r^2x-b^3+r^2b$

Let

$f(x)= (x-b)^3-r^2(x-b)=x^3-3x^2b +3b^2x-r^2x-b^3+r^2b$

then using Factor theorem,

$f(b)= b^3-3b^3 +3b^3-r^2b-b^3+r^2b=0$

$f(b)=0$

therefore $b$ is a root of the cubic equation.

 

[SammyS]

Okay using what you and @pasmith hinted,
let the roots be $(b-r), b$ and $(b+r)$
then we shall have $(x-b)(x-b-r)9x-b+r)=(x-b)[(x-b)^2 -r^2]$

Look!

If you start out saying that $b$ is one of the roots of the equation, then of course you will find that $b$ is a root of the equation.

 

[chwala]

In order to show $b$ is a root, you need to show $f(b)=0$. Notice that the only thing you can conclude from the assumption of arithmetic progression is that the roots are $b-r,b, b+r$, or $b, b+r, b+2r$. You're assuming $r=1$.

Okay using what you and @pasmith hinted,
let the roots be $(b-r), b$ and $(b+r)$
then we shall have $(x-b)(x-b-r)9x-b+r)=(x-b)[(x-b)^2 -r^2]=(x-b)^3-r^2(x-b)=x^3-3x^2b +3b^2x-r^2x-b^3+r^2b$

Let $f(x)= (x-b)^3-r^2(x-b)=x^3-3x^2b +3b^2x-r^2x-b^3+r^2b$

then,

$f(b)= b^3-3b^3 +3b^3-r^2b-b^3+r^2b=0$

$f(b)=0$ using Factor theorem and therefore $b$ is a root of the cubic equation.

Look!

If you start out saying that $b$ is one of the roots of the equation, then of course you will find that $b$ is a root of the equation.

Okay boss ... I'll replace (amend) the $b$ with another letter... will do this later. Cheers...

 

[SammyS]

I've done some minor editing to the quoted parts:

Okay --- ... I'll replace (amend) the $b$ with another letter... will do this later. Cheers...

... using what you ( WWGD ) and @pasmith hinted,
let the roots be $(b-r), b$ and $(b+r)$
then we shall have $(x-b)(x-b-r)(x-b+r)=(x-b)[(x-b)^2 -r^2]=(x-b)^3-r^2(x-b)=x^3-3x^2b +3b^2x-r^2x-b^3+r^2b$

Let $f(x)= (x-b)^3-r^2(x-b)$

$\quad\quad\quad\quad=x^3-3b\,x^2 +3b^2x-r^2x-b^3+r^2b$

You have done most of the necessary algebra. We might as well use the variable, $p$ rather than using $b$ in ensuring that we have an arithmetic progression. The variable, $r$, is fine to use.

Then you have that $(p-r),\, p$ and $(p+r)$ are zeros of the following cubic polynomial.

$\displaystyle f(x)= (x-p)^3-r^2(x-p)$

$\displaystyle \quad\quad\quad=x^3-3p\,x^2 +3p^2x-r^2x-p^3+r^2p$

We need this polynomial to be identical to the given polynomial. Therefore, we must have that

$\displaystyle f(x)=x^3-3bx^2+cx-d$

This implies that the corresponding coefficients must be equal respectively. In particular, the coefficient of $x^2$ in the first version of $f(x)$ must be equal to the coefficient of $x^2$ in the second version.

Edit: -to reword/replace the following sentence.
Does this show that $b$ is a root of the cubic equation in the given problem?

This does show that $b$ is a root of the given cubic equation, given that the roots are in arithmetic progression.

 

[chwala]

I've done some minor editing to the quoted parts:

You have done most of the necessary algebra. We might as well use the variable, $p$ rather than using $b$ in ensuring that we have an arithmetic progression. The variable, $r$, is fine to use.

Then you have that $(p-r),\, p$ and $(p+r)$ are zeros of the following cubic polynomial.

$\displaystyle f(x)= (x-p)^3-r^2(x-p)$

$\displaystyle \quad\quad\quad=x^3-3p\,x^2 +3p^2x-r^2x-p^3+r^2p$

We need this polynomial to be identical to the given polynomial. Therefore, we must have that

$\displaystyle f(x)=x^3-3bx^2+cx-d$

This implies that the corresponding coefficients must be equal respectively. In particular, the coefficient of $x^2$ in the first version of $f(x)$ must be equal to the coefficient of $x^2$ in the second version.

Does this show that $b$ is a root of the cubic equation in the given problem?

@SammyS thanks so much for your invaluable contribution... got busy with work...will check on thread later boss.