- #1
OwlsInATrenchcoat
- 4
- 1
- Homework Statement
- A swimmer is drowning at B, a distance a/2 = 10m away from the beach.
A lifeguard patrolling along the very edge of the beach spots the swimmer when the lifeguard is at point A, which is a distance a=20m away from the point on the beach that is closest to the drowning swimmer.
The average speed of the lifeguard running along the beach is v = 8ms^-1
and her average swimming speed is v=8/3ms^-1
What is the minimum time that the lifeguard can reach the swimmer?
- Relevant Equations
- Speed = distance / time
a^2 = b^2 +c^2 for a right angled triangle.
.
Hello all,

I've solved this problem on IP by writing the relevant equations into Gsheets and solving through trial and error. I've followed their hints for solving it, which lead me to a rather complex quadratic to solve. I'd appreciate if anyone can give me a clue as to how to solve for x in the following:
0 = -1/8 + 3/8 x / (10^2 +x^2)^0.5
The logic behind that is that the total time will be given by:
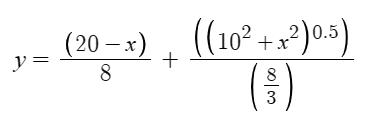
If x is the distance from O to C, where C is the point along the beach that they stop running and begin swimming. The first term is the time taken to run to C, and the second to swim along the hypotenuse of triangle OBC.
Graphing this we can see a curve, where the minimum value is a point where the gradient is 0.
So differentiating and equating to zero, we get:
0 = -1/8 + 3/8 x / (10^2 +x^2)^0.5
I'm fairly happy with all of that logic, and the value of x = 3.536m giving t = 6.035533909s checks out on IP and when input into the above equations, so I'm pretty sure my rearrangement and differentiation is OK.
So, it's just the last step, solving for x. I've tried rearranging and inputting into the quadratic formula, but I get a negative discriminant. I'd greatly appreciate anyone walking through that last step. My algebra is clearly rusty!
Or if you can see a different approach to reach the same solution, that would also be interesting. :)
Many thanks,
PP
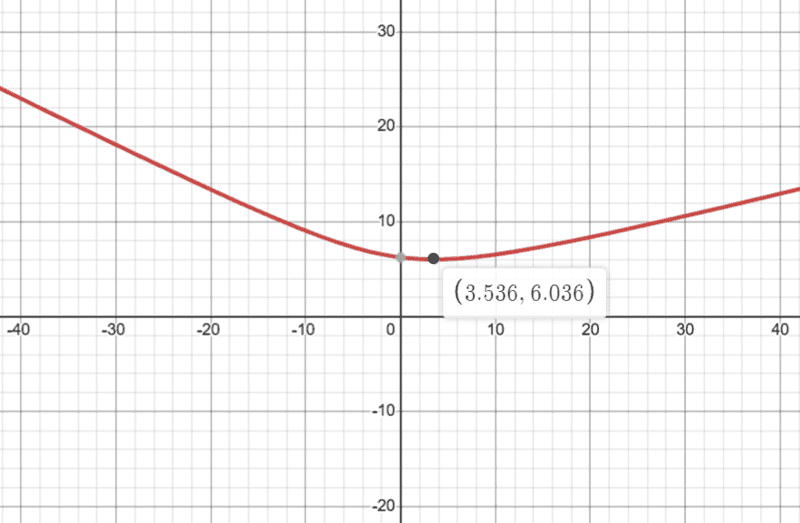

I've solved this problem on IP by writing the relevant equations into Gsheets and solving through trial and error. I've followed their hints for solving it, which lead me to a rather complex quadratic to solve. I'd appreciate if anyone can give me a clue as to how to solve for x in the following:
0 = -1/8 + 3/8 x / (10^2 +x^2)^0.5
The logic behind that is that the total time will be given by:
If x is the distance from O to C, where C is the point along the beach that they stop running and begin swimming. The first term is the time taken to run to C, and the second to swim along the hypotenuse of triangle OBC.
Graphing this we can see a curve, where the minimum value is a point where the gradient is 0.
So differentiating and equating to zero, we get:
0 = -1/8 + 3/8 x / (10^2 +x^2)^0.5
I'm fairly happy with all of that logic, and the value of x = 3.536m giving t = 6.035533909s checks out on IP and when input into the above equations, so I'm pretty sure my rearrangement and differentiation is OK.
So, it's just the last step, solving for x. I've tried rearranging and inputting into the quadratic formula, but I get a negative discriminant. I'd greatly appreciate anyone walking through that last step. My algebra is clearly rusty!
Or if you can see a different approach to reach the same solution, that would also be interesting. :)
Many thanks,
PP