- #1
Amrator
- 246
- 83
- Homework Statement
- A train with proper length ##L## and speed ##\frac{3c}{5}## approaches a tunnel with length ##L##. At the moment the front of the train enters the tunnel, a person leaves from the front of the train and walks (briskly) toward the back. She arrives at the back of the train right when it (the back) leaves the tunnel.
a) How much time does this take in the ground frame?
b) What is the person's speed with respect to the ground?
c) How much time elapses on the person's watch?
- Relevant Equations
- $$t_{observed} = \gamma t_{proper}$$
$$L_{observed} = \frac{L_{proper}} {\gamma}$$
$$t_R - t_L = \frac{Lv}{c^2}$$
$$V = \frac{u+v}{1+\frac{uv}{c^2}}$$
I've gone back to review special relativity in preparation for GR. I apologize for the horrific handwriting.
a) So the ground frame measures the length of the train to be contracted by ##\frac{4}{5}##. So ##L_G = \frac{4L}{5}##. To calculate the total distance the train travels in the ground frame, I simply added the length of the train + length of the train + (the length of the tunnel - the length of the train). This yields ##\frac{9L}{5}##. I then divided this length by the speed of the train to get the time ##\frac{3L}{c}##, which I think is the duration for her to walk from the front of the train to the back of the train in the ground frame. Is this correct?
b) I multiplied ##L_G## by the result above which gives me ##\frac{4c}{5}##. This makes no sense; in the ground frame, the person has to be moving way faster than this. What am I doing wrong?
c) I'm not even sure what this question is asking. Does it want me to find the reading of her clock in the ground frame? I'm guessing I use time dilation then.
Thank you.
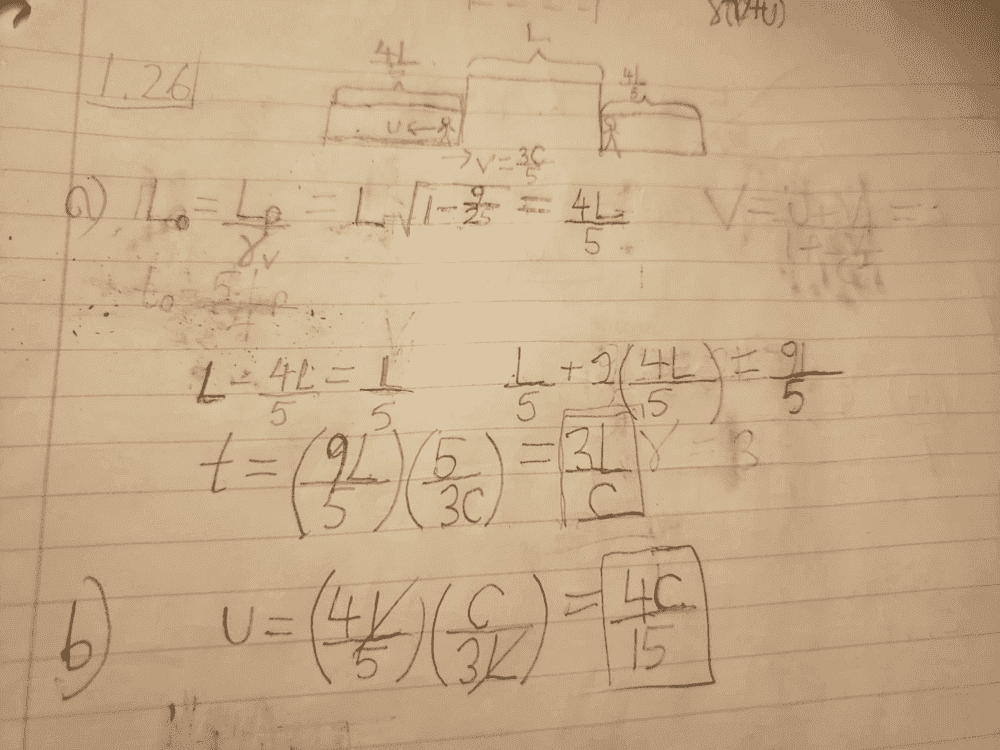
a) So the ground frame measures the length of the train to be contracted by ##\frac{4}{5}##. So ##L_G = \frac{4L}{5}##. To calculate the total distance the train travels in the ground frame, I simply added the length of the train + length of the train + (the length of the tunnel - the length of the train). This yields ##\frac{9L}{5}##. I then divided this length by the speed of the train to get the time ##\frac{3L}{c}##, which I think is the duration for her to walk from the front of the train to the back of the train in the ground frame. Is this correct?
b) I multiplied ##L_G## by the result above which gives me ##\frac{4c}{5}##. This makes no sense; in the ground frame, the person has to be moving way faster than this. What am I doing wrong?
c) I'm not even sure what this question is asking. Does it want me to find the reading of her clock in the ground frame? I'm guessing I use time dilation then.
Thank you.