Spin density in an (ideal) Fermi gas

[dRic2]

TL;DR Summary

Notation used:

With $n_m( \mathbf x) = \hat \psi_m^{†}( \mathbf x) \hat \psi_m( \mathbf x)$ I mean the density of the particle with spin $m$ and $\psi_m^{†}$ $\hat \psi_m$ are the field operator

$|F>$ = (ground) state of a ideal fermi gas (no interaction)

Hi,

some time ago our professor told us (en passant) to evaluate this quantity:
$$<F|n_m( \mathbf x) n_{m'}(\mathbf x) |F> - <F|n_m( \mathbf x)|F><F|n_{m'}(\mathbf x) |F>$$
And then he said: "you'll find that this quantity may not be zero. In particular when the electron are correlated it will not be zero." Then he said something about the spin of the electrons being "parallel". I'm really sorry if I'm being vague but I really don't remember because it was some time ago. Anyway... I calculated the first part using Wick's theorem and I got:
$$<F|n_m( \mathbf x) n_{m'}(\mathbf x) |F> = <F|\hat \psi_m^{†}( \mathbf x) \hat \psi_m( \mathbf x) \hat \psi_{m'}^{†}( \mathbf x) \hat \psi_{m'}( \mathbf x) |F>=$$
$$ =<F|\hat \psi_m^{†}( \mathbf x) \hat \psi_m( \mathbf x)|F><F|\hat \psi_{m'}^{†}( \mathbf x) \hat \psi_{m'}( \mathbf x) |F> + <F|\psi_m^{†}( \mathbf x) \hat \psi_{m'}( \mathbf x)|F><F|\psi_m( \mathbf x) \hat \psi_{m'}^{†}( \mathbf x)|F> =$$
$$= <F|n_m( \mathbf x)|F><F|n_{m'}(\mathbf x) |F> + <F|\psi_m^{†}( \mathbf x) \hat \psi_{m'}( \mathbf x)|F><F|\psi_m( \mathbf x) \hat \psi_{m'}^{†}( \mathbf x)|F>$$
So the interesting quantity is:
$$<F|\psi_m^{†}( \mathbf x) \hat \psi_{m'}( \mathbf x)|F><F|\psi_m( \mathbf x) \hat \psi_{m'}^{†}( \mathbf x)|F>$$
which I can re-write in momentum base as (I didn't use vector notation here sorry):
$$<F| \sum_{kk'} e^{(k-k')x} c_{k,m}^{†} c_{k',m'}|F><F|\sum_{qq'} e^{(q-q')x} c_{q,m} \hat c_{q',m'}^{†}|F>$$

Is it okay ?

Because from here I don't really see what kind of conclusion I could draw... The only thing I could think of is the following:
in order for that term not to vanish I should have (correct me if I'm wrong) a state with the energy levels filled like this:

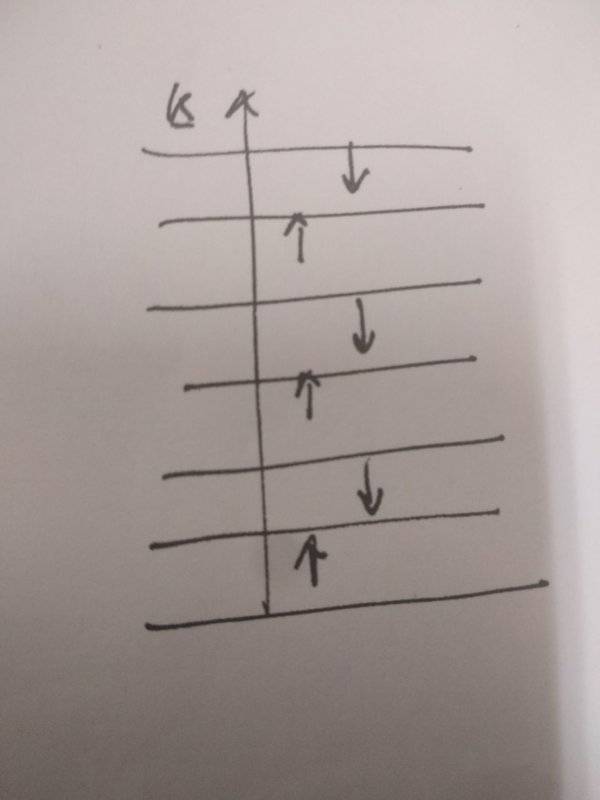
Does it make sense ? Is there something more one can say about this ?

I'm again very sorry if it all seems vague but I can't remember and I hope that maybe some of you can recognize it as a well know example or something...

Thanks
Ric

 

[eljose79]

ardo

Dear Ricardo,

Thank you for sharing your thoughts and calculations on this quantity. It seems like you have a good understanding of the mathematics involved, but I would like to clarify a few things for you.

Firstly, the quantity you are evaluating is known as the "two-particle density matrix" and it is used to describe the correlation between two particles in a system. When this quantity is not equal to zero, it means that the two particles are correlated in some way. This is often seen in systems where the particles have a parallel spin, as your professor mentioned.

In terms of your calculations, it looks like you have correctly applied Wick's theorem and have arrived at the correct expression for the two-particle density matrix. However, I would recommend using vector notation for clarity, as you mentioned in your post.

As for your conclusion, you are correct in saying that for this quantity to not vanish, the energy levels must be filled in a specific way. Specifically, the two particles must be in a state where one has a spin up and the other has a spin down, and both are in the same energy level. This is known as a "spin-singlet" state.

I hope this helps clarify some things for you. Keep up the good work in your studies!