Supremum proof & relation to Universal quantifier

[CGandC]

TL;DR Summary

x

In the following proof:

I didn't understand the following part:

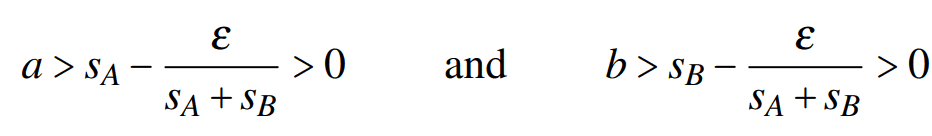
Isn't it supposed to be :
$a > s_A - \epsilon >0$ and $b > s_B - \epsilon >0$

Because to prove that $s$ is a supremum, we need to prove the following:
For every $\epsilon > 0$ there exists $m \in M$ such that $m > s - \epsilon$ .

So In my proof, to represent the claim for $a \in A$ I do the following:
Let $\epsilon > 0$ be arbitrary. Define $m=a$ . Then we need to prove $a > s_A - \epsilon$ . ( where $s_A$ is my upper bound for $A$ )

However, I didn't understand why they wrote $\frac{\epsilon}{s_A + s_B}$ instead of $\epsilon$ . They prove $a > s_A - \frac{\epsilon}{s_A + s_B}$ but I don't understand how they replaced the $\epsilon$ with $\frac{\epsilon}{s_A + s_B}$ since the universal quantifier in the proof is on $\epsilon$ and not on $\frac{\epsilon}{s_A + s_B}$ . Can you please help me understand why they did this?

Note: I saw this kind of bound variable manipulation appearing also in the following:
$\forall n \in N ( n < s)$ is the same as $\forall n \in N ( (n+1)<s )$ ( 'N' is the natural numbers set , 's' is some free variable )
Why is this possible?

 

[mathman]

It's just another $\epsilon$, since it is supposed to hold for every $\epsilon \gt 0$.

 

[CGandC]

So in my proof I write as follows? :
Let $\frac{\epsilon}{s_A + s_B} > 0$ be arbitrary. Define $m=a$ . Then we need to prove $a > s_A - \frac{\epsilon}{s_A + s_B}$ . ( where $s_A$ is my upper bound for $A$ )

OR

Let $\epsilon > 0$ be arbitrary. Define $m=a$ . Then we need to prove $a > s_A - \frac{\epsilon}{s_A + s_B}$ . ( where $s_A$ is my upper bound for $A$ )

but these don't look correct. Can you please elaborate?

 

[Office_Shredder]

Why are you proving a is bigger than something? You're supposed to assume it. Let $\delta = \frac{\epsilon}{s_a+s_b}$. Then since $\delta>0$, there exists some $a$ such that $s_a > a > s_a- \delta$.

 

[CGandC]

Why are you proving a is bigger than something? You're supposed to assume it. Let $\delta = \frac{\epsilon}{s_a+s_b}$. Then since $\delta>0$, there exists some $a$ such that $s_a > a > s_a- \delta$.

I was just giving an example of what I would write if I had to prove that given $s_a$ is supremum given it is an upperbound. I'm trying to get used to math proofs.

So what you've done is you introduced 2 arbitrary variables, like so?:
Let $\epsilon > 0$ . Let $\delta = \frac{\epsilon}{s_a+s_b}$.
Then I write like you did:
Then since $\delta > 0$, there exists some $a$ such that $s_a > a > s_a - \delta$

 

[Office_Shredder]

Right. The idea is that you know $s_a$ is a supremum, so you can pick a as close as you want to it. In the definition of the supremum, "as close as you want" is defined to be $\epsilon$, but in practice in proofs you typically have some other expression possibly involving a variable named $\epsilon$ that you use as your "as close as you want" number.