Surface area of inner and outer halves of torus

[TheCanadian]

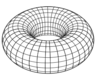
A torus with major radius, $R$, and minor radius, $r$, has a total surface area given by $4\pi^2 Rr$. If one slices the torus on its midline (i.e. at a line on a poloidal angle of $-\pi/2$ and $\pi/2$), I was told the inner half of the torus has a smaller surface area than the outer half of the torus.

Although I am having some trouble visualizing this. If we were to simply cut the torus at one point and stretch it out, it would simply look like a cylinder, where the inner and outer halves have equal surface areas. But in this case, the curvature supposedly changes that. Any insight on why exactly the surface area changes for the inner and outer halves, and how one can quantify the change in surface area due to curvature in this case, would be greatly appreciated.

 

[mfb]

If we were to simply cut the torus at one point and stretch it out, it would simply look like a cylinder

You can't do that while preserving areas and the overall geometry (e. g. keeping the separation between the outer and inner half on opposite sides).

 

[TheCanadian]

You can't do that while preserving areas and the overall geometry (e. g. keeping the separation between the outer and inner half on opposite sides).

It seems like this is where my misunderstanding lies. Would you happen to have a visualization or any equations describing why the areas are not preserved?

It seems fairly simply that: $A = (2\pi r)(2\pi R) = 2\pi r L$ which is the same equation as the area of a cylinder of length, $L = 2\pi R$, which you would get if the cylinder was fully cut in one toroidal cross-section and made straight. What's the error in this interpretation?

 

[Nidum]

 

[mfb]

Alternatively, consider the distance between the small circles on the inside and outside here:

The total area corresponds to a cylinder with 2 pi R length, but the torus doesn't consist of many small cylinders.

 

[mathman]

To simplify the visualization, consider a cut by a plane perpendicular to the torus axis. You get two circles, one from the inner half and one from the outer half. The outer circle is longer than the inner circle. Integrate over all such plane cuts and the small circles total area is smaller than the large circles total area. These correspond to the cut you made.

 

[lavinia]

The inner and outer circles are of different length. If you cut the torus and straightened it out into a cylinder, these two cut circles would become line segments of equal length. That means stretching/shrinking has happened.

- In four dimensions, one can make a torus where the two halves have equal area - although in four dimensions the idea of inner and outer goes away. In this case the cut torus can be straightened into a cylinder without stretching or shrinking. It is truly a geometric double cylinder. This torus has zero Gauss curvature.

 

[mfb]

- In four dimensions, one can make a torus where the two halves have equal area - although in four dimensions the idea of inner and outer goes away. In this case the cut torus can be straightened into a cylinder without stretching or shrinking. It is truly a geometric double cylinder. This torus has zero Gauss curvature.

In case someone is wondering how that looks like: Imagine a long strip of paper flat on the ground. If you want to connect its ends in two dimensions, you have to stretch one side or shrink the other to make a shape like this:

In three dimensions, you can produce this without any stretching:

In 4 dimensions you can do the equivalent to the second thing with a cylinder instead of a strip of paper because the cylinder is "flat" in the fourth dimension.