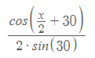- #1
Jane Smith
- 12
- 1
Homework Statement
For a physics experiment I need to find the uncertainties and I am using the angle of minimum derivation formula:

The value of A=60° and one of the values of D is 29.7° which has a uncertainty of ±2 (I know it's a very high value)
Homework Equations
How do I calculate the uncertainty for this?
The Attempt at a Solution
I found a video which included some formulas but I did not understand (attached photos)