- #1
Worn_Out_Tools
- 4
- 1
I encountered a question which asked me to describe the rose petal sketched below in polar coordinates. The complete answer is
R = {(r, θ): 0 ≤ r ≤ 6 cos(3θ), 0 ≤ θ ≤ π}. That makes sense to me for the right petal. What about the other two on the left?
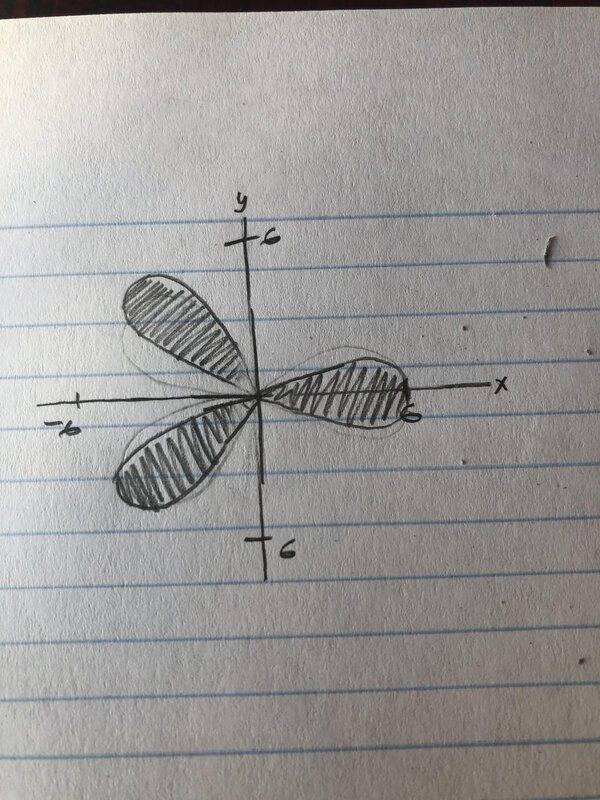
R = {(r, θ): 0 ≤ r ≤ 6 cos(3θ), 0 ≤ θ ≤ π}. That makes sense to me for the right petal. What about the other two on the left?