Vertical beam on a frictionless surface

[Arjan82]

This could also be posted in the Math / differential equations sub, but it also involves the derivation which is classical physics. So I was doubting .

So, I'm dusting off my dynamics a bit and found this problem of a thin beam on a frictionless surface in a different forum and decided to have a crack at it:

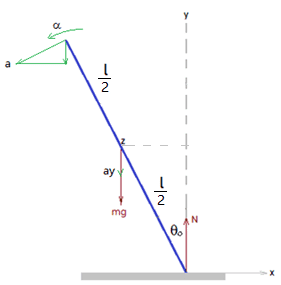
The surface is frictionless, so the end of the beam on the surface will slide to the right when it is released. What is the normal force / reaction force $N$? This is the derivation of the differential equations:

First the relation between $\theta(t)$ and $y(t)$, the latter is measured at the middle of the beam:
$$ y = \frac{l}{2}\cos(\theta) $$
$$\dot{y} = - \frac{l}{2}\sin(\theta) \dot{\theta}$$
$$\ddot{y} = - \frac{l}{2}\left(\dot{\theta}^2\cos(\theta) + \ddot{\theta}\sin(\theta)\right)$$

We have a coupled system for vertical force and momentum (positive CCW), so we need $\Sigma F_y = ma_y$ and $\Sigma M = I\alpha$:
$$ \Sigma F_y = N - mg = m\ddot{y} = - m\frac{l}{2}\left(\dot{\theta}^2\cos(\theta) + \ddot{\theta}\sin(\theta)\right)$$

For the sum of the moments we take the point at the middle of the beam such that gravity falls out. Also, then we can take the moment of inertia around the center, $I_m = 1/12ml^2$, so in this case:
$$ \Sigma M = \frac{l}{2}N\sin(\theta) = I_m\ddot\theta = \frac{1}{12}ml^2\ddot{\theta}$$
And here is our system of equations describing the beam, two equations ($\Sigma F_y$ and $\Sigma M$) with two unknowns ($N(t)$ and $\theta(t)$). Now solving these coupled non-linear differential equations analytically is hard if not impossible (I guess?!?).

Some questions:

1. You can solve the $\Sigma M$ equation for $\ddot{\theta}$ and substitute in the $\Sigma F_y$ equation. If you then also take as initial condition $\dot{\theta} = 0$ and $\theta = \theta_0$ you end up with: $$N = \frac{mg}{1+3\sin^2(\theta_0)}$$ This would suggest that the initial condition for $N$ is not free to chose because otherwise it would lead to inconsistencies. But I would guess that to solve this equation you need an initial condition for $N(t)$, $\theta(t)$, $\dot{\theta}(t)$ and $\ddot{\theta}(t)$ (in fact, I want to solve this in Matlab for which I need to rewrite everything in a system of 4 equations which need 4 initial conditions...). This is paradoxical to me, what am I missing? (In fact, in the other forum (Dutch) the OP asked for the normal force $N$ directly after the beam is released and got this answer, which would suggest it is fixed)
2. I'm guessing this is not the only or perhaps not even the easiest way to do this? Are there better ways? With energy conservation maybe? I seem to remember this was also possible.
3. Is there some opensource software you can model this in and get the answers as a check? I've found HOTINT but I'm not yet able to get the reaction force out of this (only kinematics, i.e. speeds and accelerations). I've tried to solve this in Matlab (the ode45 solver) but hopelessly failed thus far...

 

[Twigg]

I think you have the right idea with energy conservation. With energy conservation, I get a single nonlinear first-order ODE, suitable for good ol' Runge-Kutta methods on your favorite numerical platform. The energy should have 3 terms: one gravitational potential term, one linear kinetic term on the y-axis, and one rotational kinetic term. Solve for $\dot{\theta}$, then let numerics tackle the rest. Once you have the numerical results, you can calculate y vs t, and from that you can calculate the net force, take out the mg and you have the normal force.

Let me know if you want me to write up what I got.

 

[Arjan82]

I'll try, but you need at least two equations because you have two unknowns ($N$ and $\theta$)...?

 

[A.T.]

Summary:: An (almost) vertical rigid beam is put on a horizontal surface and released. What is the reaction force of the surface?

The surface is frictionless, so the end of the beam on the surface will slide to the right when it is released.

Potentially relevant (the first 15:30 min):

https://www.coursera.org/lecture/ s...inetics/8-2-example-slender-rod-falling-BMZ0q

 

[BvU]

Interesting lecture (the chap talks rocket fast, but is articulate enough, fortunately ) !
I have a slight problem understanding why there is no objection against $\mathbf{\dot H_c=L_c}$ in the CM system - which is not inertial. Must be ok, but isn't a priori obvious to me.

Apart from that the EOM

should be a breeze for ode45.

Interesting to find out when (if?)

goes to zero at some $\theta < {\pi\over 2}$ and we get a different EOM

 

[Twigg]

I'll try, but you need at least two equations because you have two unknowns ($N$ and $\theta$)...?

Yep! My two equations are (1) energy conservation and (2) $\sum F_y = m\ddot{y}$. Energy conservation gives me $\dot{\theta}(\theta)$, numerics integrate that to give me $\theta(t)$, and $\sum F_y = m\ddot{y}$ gives me the normal force. Alternatively, you could use $\sum M = I\ddot{\theta}$ instead of $\sum F_y = m\ddot{y}$. The choice is yours!

 

[Twigg]

Potentially relevant (the first 15:30 min):

https://www.coursera.org/lecture/ s...inetics/8-2-example-slender-rod-falling-BMZ0q

From 13:30ish on is the same as what I got. Definitely the easier approach.

 

[etotheipi]

I have a slight problem understanding why there is no objection against H˙c=Lc in the CM system - which is not inertial. Must be ok, but isn't a priori obvious to me.

I haven't watched the video but I'm guessing it's because inertial forces that arise in the centre of mass frame have zero torque about the centre of mass.

But anyway, you could also choose some coordinates e.g. the $x$-position of the point of contact, $x$, and the angle to the vertical, $\theta$, write the velocity of the centre of mass in terms of these coordinates, and then come up with a lagrangian$$\mathcal{L} = \frac{1}{2}m\dot{x}^2 - \frac{1}{2}ml\dot{x}\dot{\theta} \cos{\theta} + \frac{1}{6}ml^2 \dot{\theta}^2 - \frac{1}{2}mgl\cos{\theta}$$and then obtain two equations of motion. Maybe faster than using forces [so long as I didn't mess up]

 

[Arjan82]

Allright, got my answers

Referring to the questions in my first post:

1. Apparently I was wrong. You only need two initial conditions, one for initial speed and one for initial condition. The initial normal force as computed with the ode45 solve (python this time) matches exactly the formula given earlier: $$N = \frac{mg}{1+3\sin^2(\theta_0)}$$
2. As you can see in the plot above the angular velocity as computed matches almost perfectly with the result from the energy equation, which is algebraic and thus much easier: $$\dot{\theta}^2 = \frac{12g(1-\cos\theta)}{L(1+3\sin^2\theta)}$$
3. Well, I haven't found this one yet, but I can check the angular velocity and the time at the angle $\pi$, which match very well with the result from HOTINT

 

[Arjan82]

By the way the difference at t = 0 between the ODE solution and the energy equation (right plot) is due to the initial angle of 1deg in de ODE which is infinitesimal in the energy equation.