What is the acute angle at $P$ where lines $(AG)$ and $(HB)$ intersect?

[karush]

The following diagram show a solid figure ABCDEFGH. Each of the six faces is a parallelogram

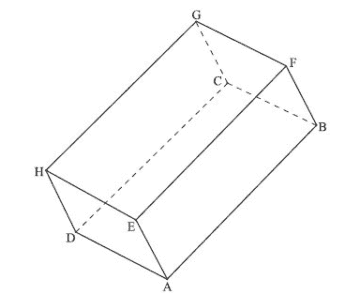
The coordinates of A and B are A(7,−3,−5),B(17,2,5)

$\vec{AB} = \langle 17-7, 2+3, 5+5 \rangle = \langle 10, 5, 10 \rangle$

$|AB|= \begin{align*} \sqrt{ (17 - 7)^2 + [2 - (-3)]^2 + [5 -(-5)]^2} \end{align*}=15$

The following information is given

$\vec{AD}=\left[ \begin{array}{c} -6 \\ 6 \\3 \end{array} \right]$ , $|AD|=9$ , $\vec{AE}=\left[ \begin{array}{c} -2 \\ -4 \\4 \end{array} \right]$ , $|AE|=6$

I assume the following is Dot product
$A\cdot B = a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$

Calculate $A\cdot B$

$-6\cdot -2+6\cdot -4+3\cdot 4=0$

thus $A\perp B$

more ? to come just seeing if this is correct:D

 

[MarkFL]

It looks as though you have calculated (with a typo, but the correct result):

$$\overrightarrow{AD}\cdot\overrightarrow{AE}=0$$

Is this correct?

 

[karush]

(ii) Calculate $\vec{AB}\cdot\vec{AD}$

$\left[ \begin{array}{c} 10 \\ 5 \\ 10 \end{array} \right]\cdot \left[ \begin{array}{c} -6 \\ 6 \\ 3 \end{array} \right]$ $10(-6)+5(6)+10(3)=0$

(iii) Calculate $\vec{AB}\cdot\vec{AE}$

$\left[ \begin{array}{c} 10 \\ 5 \\ 10 \end{array} \right]\cdot \left[ \begin{array}{c} -2 \\ -4 \\ 4 \end{array} \right]$ $10(-2)+5(-4)+10(4)=0$

$\vec{AB}\perp \vec{AD}$ and $\vec{AB}\perp \vec{AE}$ since dot products $= 0$

(c) Calculate the volume of the solid $ABCDEFGH$

since $|\vec{AB}|=15$, $|\vec{AD}|=9$, $|\vec{AE}|=6$ then $V=(15)(9)(6)=810$ units$^2$

 

[karush]

https://www.physicsforums.com/attachments/1039
(d) The coordinates of $G$ are $(9, 4, 12)$ Find the coordinates of $H$

Since $\vec{AB} = \left[ \begin{array}{c} 10 \\ 5 \\ 10 \end{array} \right]$

then can we take G and subtract $\vec{AB}$ from it get $H$

$\left[ \begin{array}{c} 9 \\ 4 \\ 12 \end{array} \right]-\left[ \begin{array}{c} 10 \\ 5 \\ 10 \end{array} \right]=\left[ \begin{array}{c} -1 \\ -1 \\ 2 \end{array} \right]$

there is one more question to this but want to see if so far is correct...

 

[Prove It]

https://www.physicsforums.com/attachments/1039
(d) The coordinates of $G$ are $(9, 4, 12)$ Find the coordinates of $H$

Since $\vec{AB} = \left[ \begin{array}{c} 10 \\ 5 \\ 10 \end{array} \right]$

then can we take G and subtract $\vec{AB}$ from it get $H$

$\left[ \begin{array}{c} 9 \\ 4 \\ 12 \end{array} \right]-\left[ \begin{array}{c} 10 \\ 5 \\ 10 \end{array} \right]=\left[ \begin{array}{c} -1 \\ -1 \\ 2 \end{array} \right]$

there is one more question to this but want to see if so far is correct...

I agree with this answer :)

 

[karush]

(d) The lines $(AG)$ and $(HB)$ intersect at $P$
and given that
$\vec{AG}=\left[ \begin{array}{c} 2 \\ 7 \\ 17 \end{array} \right]$

find the acute angle at $P$

$\vec{HB}=(-1,-1,2) + (17,2,5) = (16,1,7)$ and $|AG|=3\sqrt{38}$

then

$COS^{-1}\left(\frac{\vec{AG}\cdot\vec{HB}}{(3\sqrt{38})^2}\right) \approx 62.38^o$