- #1
vcsharp2003
- 897
- 176
- Homework Statement
- A particle P, as shown in diagram below, is moving at a velocity of ##2 \hat i \, {m/s}## at time ##t=0## under a constant acceleration of ## 2 \hat i - 2 \hat j \, m/s^2 ##. Would the particle move in a circular path? Provide explanation.
- Relevant Equations
- ## F_c= \dfrac {mv^2} {r}##
## a_t= \alpha r##
At t= 0, we can see that the particle P has a radial acceleration of ##-2\hat j## and a tangential acceleration of ##2 \hat i##. The radial acceleration will tend to move it in a circle of a certain radius, whereas the tangential acceleration will tend to displace it parallel to x- axis.
Consider a very small interval of time after the time t = 0. At the end of this very small interval of time, the vector sum of above two displacements is not going to be on a circle as shown in diagram below. In this diagram, the displacements due to tangential and radial accelerations are shown as ##d_2## and ##d_1## respectively after a very small time interval from t = 0. We can see that net displacement is going to place the particle slightly above the circular path and therefore, the particle will not move along a circular path.
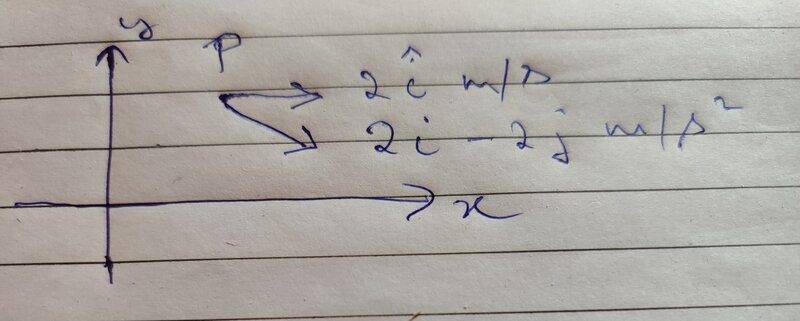

Consider a very small interval of time after the time t = 0. At the end of this very small interval of time, the vector sum of above two displacements is not going to be on a circle as shown in diagram below. In this diagram, the displacements due to tangential and radial accelerations are shown as ##d_2## and ##d_1## respectively after a very small time interval from t = 0. We can see that net displacement is going to place the particle slightly above the circular path and therefore, the particle will not move along a circular path.
Last edited: