Calculating Net Charge Inside a Cube in an Electric Field

[Antonius]

Homework Statement

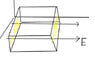
A large cube has its bottom face on the x-z plane and its back face on the x-y plane. The corners on the x-axis are at (7.93 m,0,0) and (15.9 m,0,0). The cube is immersed in an electric field pointing in the positive x-direction, and given by:

E = (44.9x2 - 9.92)i, x is the distance along the x-axis in m, and E is in N/C.

NOTE:This means that E has constant direction, but increases in magnitude with the x-coordinate.

Find the net charge Q inside the cube, in μC.

NOTE: The sign of the charge is important!

Homework Equations

E * A = Q enclosed / ε

3. The Attempt at a Solution

E = ( 44.9 x^2 - 9.92 ) i

My first task is to find Electric field so I can use the formula that is provided in the Relevant Equations section. My question is more about math rather physics. Am I allowed to conclude that E is equal to [ ∫ 44.9 x^2 - 9.92 dx ] with lower limit being 7.93 and upper limit being 15.9? If that logic is correct then there is no other question. I got Q enc = 4.5243 Coulombs ...

Thank you Ψ

 

[blue_leaf77]

My first task is to find Electric field

Find the electric field? But you have been given, haven't you?

 

[Antonius]

Find the electric field? But you have been given, haven't you?

Well that's my question :D They gave me Electric field that varies over x.
My question is, is it alright if I take the integral of this ---> ( 44.9 x^2 - 9.92 ) with lower limits and upper limits as mentioned in the "My attempt" section? :/

 

[blue_leaf77]

Gauss law reads
$$
\oint \mathbf{E}\cdot d\mathbf{a} = \frac{Q_{enc}}{\epsilon_0}
$$
So, my first question is, how do you plan on integrating ( 44.9 x^2 - 9.92 ), e.g. what will be the surface element of the surface on which you will do the integration?

My question is more about math rather physics. Am I allowed to conclude that E is equal to [ ∫ 44.9 x^2 - 9.92 dx ] with lower limit being 7.93 and upper limit being 15.9?

Let's hear your argument why you want to integrate with respect to x?

 

[Antonius]

The surface is just a number (15.9 - 7.93) * 2 * 2
and only E is changing as x increases as it says in the problem - Note that E has constant direction, but increases in magnitude with the x-coordinate...

 

[Antonius]

Isn't here where Integration comes into find the total E over the surface? :/

 

[blue_leaf77]

The surface is just a number (15.9 - 7.93) * 2 * 2

What are you calculating with this? What are those 2's?

Isn't where Integration comes into find the total E over the surface?

You mean the integral $\oint \mathbf{E} \cdot d\mathbf{a}$? No, this integral is the total electric field flux going through a given surface. Your electric field has been given, you don't and should not find the field anymore. What you really want to calculate is the integral above, with the surface being all six walls of the cube.

 

[Antonius]

What are you calculating with this? What are those 2's?

You mean the integral $\oint \mathbf{E} \cdot d\mathbf{a}$? No, this integral is the total electric field flux going through a given surface. Your electric field has been given, you don't and should not find the field anymore. What you really want to calculate is the integral above, with the surface being all six walls of the cube.

The 2's are two sides of the cube through which the Electric Field lines pass.

I am given the formula for E.
Where in the question do you see E that I can take and just plug in and get the final result? lol ...

 

[Antonius]

With the surface being all six walls of the cube.? No ... that should not be correct ...

 

[blue_leaf77]

I got Q enc = 4.5243 Coulombs ...

Can you show your calculation to get that number?

With the surface being all six walls of the cube.? No ... that should not be correct ...

In general you have to take all surfaces into account, however in your problem the E field is parallel to some of the surfaces making the flux going into those surfaces zero.

 

[Antonius]

Can you show your calculation to get that number?

In general you have to take all surfaces into account, however in your problem the E field is parallel to some of the surfaces making the flux going into those surfaces zero.

Yes that was my point. It's only passing through two sides on the cube, that's why I multiplied the area by 2.

Well I am not sure about my math...

I integrated (E) 44.9 x^2 - 9.92 with lower limit = 7.93 and upper limit 15.9. I got 40.2219 N/C.
Then I multiplied this by the area ((15.9 - 7.93) * 2 * 2)
After, I multiplied this by ε just to get Q enclosed = 4.5243 C . . .

 

[blue_leaf77]

I integrated (E) 44.9 x^2 - 9.92 with lower limit = 7.93 and upper limit 15.9. I got 40.2219 N/C.

This step is not correct. Ok you have known that the electric field only passes two surfaces of the cube, these are the surfaces which are perpendicular to the E field and are located at (7.93 m,0,0) and (15.9 m,0,0). Using the coordinate you are given in the problem, these two surfaces are parallel to the y-z plane. Now what you need to figure out is, since in doing the integral you need to integrate over these surfaces (separately), what will be the correct integration element?

 

[Antonius]

This step is not correct. Ok you have known that the electric field only passes two surfaces of the cube, these are the surfaces which are perpendicular to the E field and are located at (7.93 m,0,0) and (15.9 m,0,0). Using the coordinate you are given in the problem, these two surfaces are parallel to the y-z plane. Now what you need to figure out is, since in doing the integral you need to integrate over these surfaces (separately), what will be the correct integration element?

I am not sure why you are saying - you need to integrate over these surface (separately) ...

I am not getting it, if Integral ( E * dA )
then only E is variable and the area is constant ... I am not sure why the integral (equation) is wrong ... A hint? :(

 

[SammyS]

Yes that was my point. It's only passing through two sides on the cube, that's why I multiplied the area by 2.

Yes, the E-field is only passing through two sides of the cube.

Which two sides?

 

[Antonius]

Yes, the E-field is only passing through two sides of the cube.

Which two sides?

Excuse my cube but the sides which are highlighted are once through which the electric field passes.

 

[SammyS]

Isn't one of those sides at x = 7.93 and the other at x = 15.9 ?

 

[Antonius]

Isn't one of those sides at x = 7.93 and the other at x = 15.9 ?

Yes they are...

Is this where something is supposed to obvious? Well it's not ... D:

 

[SammyS]

Yes they are...

Is this where something is supposed to obvious? Well it's not ... D:

The E-field is one value over the entire surface at one of these ends, and another value over the entire surface at the other end.

No need to integrate the E-field over some range of x values.

 

[blue_leaf77]

If you elaborate the integral of the electric flux, you will write something like
$$
\oint \mathbf{E} \cdot d\mathbf{a} = \int_1 \mathbf{E}_1 \cdot d\mathbf{a}_1 + \int_2 \mathbf{E}_2 \cdot d\mathbf{a}_2 + \ldots + \int_6 \mathbf{E}_6 \cdot d\mathbf{a}_6
$$
where the subscripts in the integral sign, electric field, and the integral element denote the surface over which the integral is performed. In particular for the E field, a subscript following it means that this E field vector is that observed across the corresponding surface denoted by the subscript. Let's suppose the two surfaces which are traversed by the field perpendicularly are surface 1 and 2, the rest then do not contribute at all to the total flux and the 3rd up to 6th integral above should vanish. Leaving us with
$$
\oint \mathbf{E} \cdot d\mathbf{a} = \int_1 \mathbf{E}_1 \cdot d\mathbf{a}_1 + \int_2 \mathbf{E}_2 \cdot d\mathbf{a}_2
$$
what I suggest you to do is to express $d\mathbf{a}_1$ and $d\mathbf{a}_2$ in terms of Cartesian elements, e.g. $dx$, $dy$, and $dz$.

 

[Antonius]

I solved this problem already. As Sammy said all I had to do was [Eright + Eleft] A = Qenc / ε

Thank you all for help ΨΨΨ

 

[ehild]

I solved this problem already. As Sammy said all I had to do was [Eright + Eleft] A = Qenc / ε

It is not correct. In the integral ∫Eda, da is a vector, normal to the surface and pointing outward, with magnitude equal to the surface area. At one face of the cube E and A are parallel, at the other one, they are antiparallel, so you have to subtract the contributions instead of adding them.

 

[Antonius]

It is not correct. In the integral ∫Eda, da is a vector, normal to the surface and pointing outward, with magnitude equal to the surface area. At one face of the cube E and A are parallel, at the other one, they are antiparallel, so you have to subtract the contributions instead of adding them.

True that's why I wrote right and left. (I meant to write it as ErightA cos(0) + EleftA cos(180), hence, (Eright - E left) A.