Concentric circles are parallel?

[phya]

The straight line parallel to each other is parallel. Concentric circles are parallel,too.

As shown in figure, There is a big circle,Oa，Another one is small, Oc.They are concentric circles. AB is a straight line. AB and Oa are intersections D, AB and Oc are intersections C. EF is a straight line. EF through point D. EF tangent and Oa. GH is a straight line. GH through point C. GH tangent and Oc. R is for Oa radius. r is for Oc radius.

set
β=∠BCH, α=∠BDF, G=CD

is
∠ADO=90-α
∠BCO=90+β

According to the cosine theorem:

G^2=r^2+R^2-2rRcos(180-(90-α+90+β)
After finishing to
G^2=r^2+R^2-2rRcos（α-β） （2）

After finishing (2)
cos（α-β）=（r^2+R^2-G^2）/2rR
If R →∞，r→∞, then
cos（α-β）→1
α→β

When R → ∞， Oa is a straight line， r → ∞，Oc is a straight line，too. This is straight line parallel!Therefore, straight line parallel to the curve of the parallel is special.

After the above discussion, I still have some conclusions are as follows:

Can mutually perpendicular lines, Curve can also mutually vertical.

Flat surface can be parallel, curved surface can also be parallel to each other.

...

 

[HallsofIvy]

What do you mean by 'parallel'? There are some definitions of "parallel" in "concentric circles are parallel" is true and some in which it is not. The "usual" definition of parallel in Euclidean geometry specifically defines only "parallel lines" and so, with that definition, it is not true.

 

[phya]

What do you mean by 'parallel'? There are some definitions of "parallel" in "concentric circles are parallel" is true and some in which it is not. The "usual" definition of parallel in Euclidean geometry specifically defines only "parallel lines" and so, with that definition, it is not true.

Lines divided into curve and linear.All is not straight line.Why can't curve parallel?

 

[Ynaught?]

What do you mean by 'parallel'? There are some definitions of "parallel" in "concentric circles are parallel" is true and some in which it is not. The "usual" definition of parallel in Euclidean geometry specifically defines only "parallel lines" and so, with that definition, it is not true.

I understand the definition of parallel lines to be, when two lines in a plane equidistant part at every point and never intersecting they are parallel. Nothing in that states the lines need to be straight. Which must be the true part you refer to. But I don't see the not true part... Unless maybe that lines of latitude when viewed from the pole appear to be concentric circles but they are not parallel because they do not lie in the same plane?

 

[phya]

I understand the definition of parallel lines to be, when two lines in a plane equidistant part at every point and never intersecting they are parallel. Nothing in that states the lines need to be straight. Which must be the true part you refer to. But I don't see the not true part... Unless maybe that lines of latitude when viewed from the pole appear to be concentric circles but they are not parallel because they do not lie in the same plane?

Three-dimensional space straight line can be parallel.Three-dimensional space curved line can also be parallel.

 

[phya]

Does not intersect was not equal to that is parallel. For example, two curves do not intersect, but actually not necessarily is parallel. Two straight lines do not intersect only then possibly are parallel.

Why said that possibly is parallel? Please read in the appendix the chart. In chart two straight lines not parallel, also does not intersect. These two lines are infinite long, but they do not intersect, they are not also parallel.

 

[Mentallic]

If you have some curve y=f(x) then you can use your own definition to say that another curve y=f(x)+c where c is some non-zero constant is parallel to the other. This is generally not considered the true definition of parallel. Parallel is only used to describe lines and planes, not curves.

How are the two lines in that diagram infinitely long? You can see where they end!

 

[HallsofIvy]

Does not intersect was not equal to that is parallel. For example, two curves do not intersect, but actually not necessarily is parallel. Two straight lines do not intersect only then possibly are parallel.

Why said that possibly is parallel? Please read in the appendix the chart. In chart two straight lines not parallel, also does not intersect. These two lines are infinite long, but they do not intersect, they are not also parallel.

Read in what appendix? Again, please state your definition of "parallel"! These statements are true for some definitions of parallel and not for others. If you do not definie "parallel" people will be forced to assume you mean "parallel" as defined in Euclidean geometry where these statements you make are NOT true.

 

[Mentallic]

Read in what appendix?

He means the diagram at the end of his post.

 

[phya]

If you have some curve y=f(x) then you can use your own definition to say that another curve y=f(x)+c where c is some non-zero constant is parallel to the other. This is generally not considered the true definition of parallel. Parallel is only used to describe lines and planes, not curves.
How are the two lines in that diagram infinitely long? You can see where they end!

The definition is reflects the nature, is to the nature induction and the summary. A parallel definition kind of natural phenomenon. The curve parallel is also one kind of natural phenomenon. Should also contain this kind of phenomenon in humanity's parallel concept. A parallel key character is the distance maintains invariable. Regardless of being the straight line, the curve is so. This is the parallel essence. It is the straight line or the curve, this is unimportant.Humanity's understanding is parallel starts from the straight line, therefore the humanity is limited easily. Therefore the humanity knows the non-European geometry with difficulty.

 

[phya]

The definition is reflects the nature, is to the nature induction and the summary. A parallel definition kind of natural phenomenon. The curve parallel is also one kind of natural phenomenon. Should also contain this kind of phenomenon in humanity's parallel concept. A parallel key character is the distance maintains invariable. Regardless of being the straight line, the curve is so. This is the parallel essence. It is the straight line or the curve, this is unimportant.Humanity's understanding is parallel starts from the straight line, therefore the humanity is limited easily. Therefore the humanity knows the non-European geometry with difficulty.

 

[Mentallic]

Humanity's understanding is parallel starts from the straight line, therefore the humanity is limited easily.

You obviously don't know what the word "define" means, since we've mentioned it to you dozens of times already.

non-European geometry

lol non-Euclidean?

 

[phya]

You obviously don't know what the word "define" means, since we've mentioned it to you dozens of times already.

lol non-Euclidean?

Non-Euclidean Geometry？

 

[phya]

You obviously don't know what the word "define" means, since we've mentioned it to you dozens of times already.
lol non-Euclidean?

We may the narrow definition parallel, is also parallel is only about straight line between being parallel. But it in fact, parallel may also be generalized. Before we think the geometry only then the Euclid geometry, but does not have other geometries, now we knew that also has the non-Euclid geometry. After having discovered non-Euclid geometry, we may say that the Euclid geometry is only the narrow geometry.Not right?

 

[Mentallic]

If you don't know what euclidean geometry is, please explain what you meant by european geometry

In non-euclidean geometries such as spherical and hyperbolic geometries, we use the term "geodesics" rather than straight lines so as not to confuse the two. Since parallel lines can intersect in spherical geometry which disobeys our definition of parallel (it is assumed in these definitions that we are using euclidean geometry anyway).

The definition of parallel is not generally extended to curves, but you can make it that way if you like. This doesn't mean you are going to convince us all that the definition of parallel needs to be extended because you think it does.

 

[phya]

If you don't know what euclidean geometry is, please explain what you meant by european geometry

In non-euclidean geometries such as spherical and hyperbolic geometries, we use the term "geodesics" rather than straight lines so as not to confuse the two. Since parallel lines can intersect in spherical geometry which disobeys our definition of parallel (it is assumed in these definitions that we are using euclidean geometry anyway).

The definition of parallel is not generally extended to curves, but you can make it that way if you like. This doesn't mean you are going to convince us all that the definition of parallel needs to be extended because you think it does.

The slip of the pen is the very normal matter. Has the understanding to the geometry the human, actually does not know the non-Euclid geometry, this possible? But ridicules others because of others' slip of the pen, should not.

 

[HallsofIvy]

No one has ridiculed you. We have, however, repeatedly asked you to define what you mean by "parallel" any you have not done so.

 

[phya]

No one has ridiculed you. We have, however, repeatedly asked you to define what you mean by "parallel" any you have not done so.

Ask when the Euclid geometry how to define parallel?

 

[HallsofIvy]

I assume that English is not your first language. Euclidean geometry does NOT "define parallel". It does define "parallel line" and, as I said before, in Euclidean geometry, parallel only applies to straight lines. So apparently, in your question you are NOT talking about Euclidean geometry. I ask, for the third time, how do you define "parallel" in this question?

 

[phya]

I assume that English is not your first language. Euclidean geometry does NOT "define parallel". It does define "parallel line" and, as I said before, in Euclidean geometry, parallel only applies to straight lines. So apparently, in your question you are NOT talking about Euclidean geometry. I ask, for the third time, how do you define "parallel" in this question?

Indeed, in the Euclid geometry, parallel is between straight line being parallel. I have a question, ask, the line segment is may also be parallel? Sorry, please use is or is not replied.

 

[Mentallic]

Yes a line segment can be parallel to another line or line segment. In the study of geometry you encounter parallel line segments all the time.

 

[phya]

Yes a line segment can be parallel to another line or line segment. In the study of geometry you encounter parallel line segments all the time.

We may regard as the curve are composed of the innumerable strip small line segment, if composes two curves the corresponding line segments is each other parallel, then these two curves are also parallel?

 

[HallsofIvy]

You are now faced with the problem of determining precisely HOW you are going to "regard the curve as composed of innumerable small line segments" (there are many different ways of doing that- and they give different results) as well as telling which line segments are "corresponding". Until you tell us that (and I suspect that both tasks are much harder than you might think), no one can answer your question.

IF you define "parallel curves" by "at any point on one curve, the perpendicular to the curve at that point is also perpendicular to the second line and the distance from one curve to the other curve, measured along that line, is constant (independent of the initial point)", then, yes, concentric circles are "parallel" by that definition. But that is not the only possible definition of "parallel" and certainly is NOT the definition in Euclidean geometry.

In Euclidean geometry, "parallel" is only defined for lines and is simply, "two lines are parallel if and only if they do not intersect". If you drop the "lines" requirement and use that definition, then, yes, concentric circles are "parallel" but then so are any circles that do not intersect, or any line segments that do not intersect, whatever their angular orientation, any curves that do not intersect, etc.

(Parallel line segments is not, strictly speaking, defined in Euclidean geometry but some texts, for specialized purposes, define line segments to be "parallel" if and only if the lines they lie on are parallel.)

 

[Mentallic]

Well of course the tangents at some exact point on each curve are going to be parallel. This doesn't mean the general meaning of parallel is extended to curves as well. Parallel is only used for lines, but if you have a reason to change that meaning for yourself, then by all means do so. This isn't going to change the general understanding of the term parallel though.

 

[phya]

Yes a line segment can be parallel to another line or line segment. In the study of geometry you encounter parallel line segments all the time.

If two regular polygon's corresponding sides are mutually parallel, then these two regular polygons are parallel? If the answer is affirmative, then why the concentric circle is not parallel?

 

[phya]

You are now faced with the problem of determining precisely HOW you are going to "regard the curve as composed of innumerable small line segments" (there are many different ways of doing that- and they give different results) as well as telling which line segments are "corresponding". Until you tell us that (and I suspect that both tasks are much harder than you might think), no one can answer your question.

IF you define "parallel curves" by "at any point on one curve, the perpendicular to the curve at that point is also perpendicular to the second line and the distance from one curve to the other curve, measured along that line, is constant (independent of the initial point)", then, yes, concentric circles are "parallel" by that definition. But that is not the only possible definition of "parallel" and certainly is NOT the definition in Euclidean geometry.

In Euclidean geometry, "parallel" is only defined for lines and is simply, "two lines are parallel if and only if they do not intersect". If you drop the "lines" requirement and use that definition, then, yes, concentric circles are "parallel" but then so are any circles that do not intersect, or any line segments that do not intersect, whatever their angular orientation, any curves that do not intersect, etc.

(Parallel line segments is not, strictly speaking, defined in Euclidean geometry but some texts, for specialized purposes, define line segments to be "parallel" if and only if the lines they lie on are parallel.)

First, does not intersect is not necessarily parallel, we pay attention to 6 buildings the charts: Has two line segments in that circular plane, they do not intersect, also not parallel, we infinite enlarge this circular plane the diameter, in the circle line segment also meet the infinite extension, but they forever will not intersect, but will not be parallel.

 

[phya]

What is the parallel essence? Does not intersect, the distance maintains invariable? In my opinion the parallel essence is the distance maintains invariable, but is not does not intersect.

 

[phya]

In 25 building charts, if these two regular polygon's corresponding sides are parallel, then they are also parallel?

 

[94JZA80]

I understand the definition of parallel lines to be, when two lines in a plane equidistant part at every point and never intersecting they are parallel. Nothing in that states the lines need to be straight. Which must be the true part you refer to. But I don't see the not true part... Unless maybe that lines of latitude when viewed from the pole appear to be concentric circles but they are not parallel because they do not lie in the same plane?

i agree with your first statement that lines (or surfaces) don't need to be straight (or flat) in order to be parallel.

but your second statement is false. if you're standing at either of the Earth's poles and looking down at your feet, not only do lines of latitude appear to be concentric circles, but they also appear parallel. now i don't know if, by definition, concentric circles must lie in the same plane. but i would imagine that while some folks would argue that the circles are concentric b/c they share a common center, others might argue that they only "appear" concentric b/c they do not actually share a common center (b/c they don't all lie in the same plane) - rather their respective centers are all aligned with the axis that runs through the Earth's poles. so again, i don't know if lines of latitude are considered to be concentric by the strictest definition or not...

...but that's neither here nor there, as I'm trying to show that lines of latitude not only appear parallel, but in fact ARE parallel, despite not lying in the same plane. imagine again that you are at one of the Earth's poles staring at your feet. now imagine a straight line originating from the center of the Earth and intersecting an arbitrary point on the equator. there is exactly one point on each line of latitude that lies directly above this imaginary line that intersects the center of the Earth and the equator. take the 20th and 40th parallels (specific lines of latitude) for instance - connect the two points (one from each line of latitude) that lie directly above your imaginary line that intersects the center of the Earth and some arbitrary point on the equator. measure the distance between those two points lying on different lines of latitude and call it D. now look down at your feet again, and imagine another line intersecting the center of the earth, but this time intersecting a different point on the equator. if you find the points on the 20th and 40th parallels that lie directly above this newly constructed imaginary line, you'll find that the distance measured between them is still D. in fact, this holds for any imaginary line that intersects center of the Earth and any point on the equator. hence, the two lines of latitude at 20° and 40° respectively are equidistant everywhere, and are therefore parallel, despite not lying in the same plane. its also the reason they call them the 20th and 40th "parallels."

i can also see how the OP's argument extends from curved lines to curved surfaces. concentric spheres is a perfect example of parallel surfaces. for instance, take two concentric spheres with different radii (so that they cannot be mistaken for identical spheres). any line that intersects their common center will be orthogonal to both concentric spheres' surfaces, no matter where it intersects them. if we label the distance between those two points of intersection "D", then we find again that any line intersecting the concentric spheres' common center will produce two points (one on each sphere) a distance D apart. in other words, D = r2 - r1 (the difference in the length of one radius and the other) is the same everywhere, no matter where on the surface of each sphere we decide to take our radius measurement from. if the difference in radii is the same everywhere, then the spheres are parallel.

i guess this is just an elaboration on the OP's response to your conjecture, just in case it wasn't immediately clear why lines of latitude are parallel despite not lying in a common plane...of course, as we've seen from the responses of many others, this may all be true according to some definitions, and completely false by others. the definition of "parallel" i suppose has analogs depending on the space you're working in (2 dimensions, 3 dimensions, etc.) and their varying geometries (euclidean, non-euclidean, etc.)...i know some folks would shy away from calling anything other than straight lines in euclidean space "parallel," and would revert to describing such things as "equidistant," "similar," "congruent," etc. but i still feel that the word "parallel" better describes many of these curved lines or surfaces and their orientations with respect to one another than other words from the vocabulary of geometry, even if by definition the word "parallel" only concerns straight lines in euclidean space...

...just my 2 cents

 

[Dr Lots-o'watts]

What is the parallel essence? Does not intersect, the distance maintains invariable? In my opinion the parallel essence is the distance maintains invariable, but is not does not intersect.

The word parallel only applies to straight lines. There is no need to apply it to circles. For circles, you may say that for concentric circles, their tangents at the same angular position are parallel.

If you want a word for describing how certain curves don't intersect, you might want to create a new word. But chances are any 2 such curves you can imagine have already been described exactly already using words such as "correspond", "in phase", "equidistant" etc.

 

[phya]

The word parallel only applies to straight lines. There is no need to apply it to circles. For circles, you may say that for concentric circles, their tangents at the same angular position are parallel.

If you want a word for describing how certain curves don't intersect, you might want to create a new word. But chances are any 2 such curves you can imagine have already been described exactly already using words such as "correspond", "in phase", "equidistant" etc.

What is the parallel essence?

 

[phya]

The word parallel only applies to straight lines. There is no need to apply it to circles. For circles, you may say that for concentric circles, their tangents at the same angular position are parallel.

If you want a word for describing how certain curves don't intersect, you might want to create a new word. But chances are any 2 such curves you can imagine have already been described exactly already using words such as "correspond", "in phase", "equidistant" etc.

Before we only knew that has the Euclid geometry, that the ‘geometry’ this word specially refers to the Euclid geometry? The non-Euclid geometry may not use the ‘ geometry’ this word?

 

[Dr Lots-o'watts]

It's only a matter of vocabulary. I don't see why you want to use the word "parallel" so much.

Geometry is divided into "Euclidean geometry" and "non-euclidean geometry" for good reason.

You're saying perhaps we can now have "Euclidean parallel", "Euclidean circular parallel", "non-euclidean parallel", etc. I don't have any problem with that, but I don't see any reason why one would spend a lifetime trying to convincing every mathematician to use this new terminology.

 

[CRGreathouse]

It's difficult to extend the definition of parallel to objects other than lines (or subsets of lines containing at least two distinct points, I suppose). It's easy to see that approximating concentric circles as n-gons and taking the limit as n increases without bound (as earlier suggested on this thread) doesn't work, since the sides could be offset such that no segments are parallel to any segment in the other approximating n-gon.

What is the parallel essence? Does not intersect, the distance maintains invariable?

FWIW, the statement "parallel lines are always equidistant" (at perpendiculars) is equivalent to the parallel postulate, that is, forces you (in some sense) into Euclidean geometry.

It's not really clear how to extend the concept of equidistant to other shapes, but I don't see any problem in using it for circles. Two circles are equidistant if and only if they are concentric or both of zero radius.

 

[phya]

It's only a matter of vocabulary. I don't see why you want to use the word "parallel" so much.

Geometry is divided into "Euclidean geometry" and "non-euclidean geometry" for good reason.

You're saying perhaps we can now have "Euclidean parallel", "Euclidean circular parallel", "non-euclidean parallel", etc. I don't have any problem with that, but I don't see any reason why one would spend a lifetime trying to convincing every mathematician to use this new terminology.

We do not need to establish that many special terminology. The parallel concept is unified, is also the distance maintains invariable, regardless of this to curve, to the straight line, is to the surface, to the plane is so.

 

[Phrak]

Ya-all quite pickin' on phya. You all should know better. Good grief!

Normally, phya, in the way these things are taught, right or wrong, a vector or a line is independent of the coordinates in which they are described. It's really a matter of convention. In this convention, we assume that a line is independent of the coordinates, such as x,y and z by which we measure its parts. It has an existence of it's own, and the coordinates are a matter of choice.

You, on the other hand, are taking the opposite view. You take two parallel lines and wrap them in a circle. You are taking the coordinates as fundamental and the line is a mutable object.

In your system x-->radius and y-->an angle, so that parallel lines in in (x,y) are still parallel. There's nothing wrong with this, it's not the convention so people get confuse, but it certainly not wrong--just different, and a perspective that may have great value.

 

[phya]

“crosses outside the straight line a spot to have two straight lines and the known straight line at least parallel”, I believed that non-Euclid geometry's this view is wrong. Because, first, in the non-Euclid geometry's straight line is not in the Euclid geometry straight line, second, does not intersect was not equal to that is parallel, does not intersect regards is parallel, this has confused parallel and not the parallel concept. If we regard the circle the straight line, then may also say: Crosses outside the straight line a spot to be possible to make the innumerable strip straight line (this passes through known point, but does not intersect with known circle these circles) do not intersect with the known straight line.

 

[CRGreathouse]

“crosses outside the straight line a spot to have two straight lines and the known straight line parallel non-Euclid geometry some views is at least” wrong.

Who are you responding to?

 

[phya]

Who are you responding to?

My this reply not in view of anybody.

 

[CRGreathouse]

My this reply not in view of anybody.

I was just trying to understand the quotation marks (and, for that matter, the quotation).

 

[phya]

I was just trying to understand the quotation marks (and, for that matter, the quotation).

What not clearly do you have?

 

[phya]

Like the chart shows, nearby one rectangular plane's about two is parallel, if we become this rectangle uniplanar bending the proper circle barrel, nearby rectangular about two becomes two curves, ask that by now these two lines no longer were parallel?

 

[phya]

About curve parallel and non-Euclid geometry mistake and absolute geometry completion


First, about concentric circle parallel

May say like this that the straight line parallel is the concentric circle parallel special row, but the concentric circle parallel is the curve parallel special row. Curve parallel is general parallel, but the straight line parallel is quite special being parallel.

Below we have a look at the concentric circle the nature.

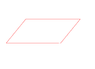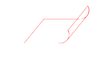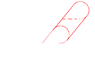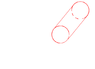
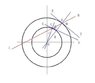
As shown in Figure 1, great-circle and small circle concentric, straight line AB and the great-circle have point of intersection C, straight line AB and the small circle have point of intersection D, straight line EF are the great-circle tangents, and D is a tangential point, straight line GH is the small circle tangent, and C is a tangential point, R is the great-circle radius, r is the small circle radius.

Supposition

β=∠BCH, α=∠BDF, β and α is the corresponding angle mutually, β is the great-circle corresponding angle, α is the small circle corresponding angle, G=CD.

Then

90-α=∠ADO
90+β=∠BCO

According to sine law:

R/sin(90+β)=r/sin(90-α)

After the reorganization,

R/cosβ=r/cosα

Reorganizes again

Rcosα=rcosβ （1）

By (1) obviously, when R and r tend infinite, the great-circle is the straight line, the small circle is also a straight line, β=α, this is also straight line being parallel. Therefore the straight line parallel is only the concentric circle parallel extreme.

According to law of cosines:

G^2=r^2+R^2-2rRcos(180-(90-α+90+β)

After the reorganization,

G^2=r^2+R^2-2rRcos（α-β） （2）

After reorganization (2) formula, obtains

cos（α-β）=（r^2+R^2-G^2）/2rR （3）

By (3) obviously, when R and r tend infinite, the great-circle is the straight line, the small circle is also a straight line, β=α (corresponding angle equal), this is also straight line being parallel. Therefore the straight line parallel is only the concentric circle parallel extreme.

We may say, in a plane, so long as G^2=r^2+R^2-2rRcos (α-β), then two circles are parallel (concentric), otherwise is not parallel (not concentric).

After the above discussion, the conclusion which I obtain is:

When straight line the line, the curve is also the line, the line including the straight line and the curve. The line may not by the understanding be a straight line merely.

In the curve, the circle is a straight line. The straight line is that kind of radius infinitely great circle.

The straight line may the mutually perpendicular, the curve also be possible the mutually perpendicular. (i.e., straight line may mutually parallel, curve may also mutually parallel). Is vertical including the straight line between vertical and between curve vertical.

The angle side may be a straight line, may also be the curve, the angle including the linear angle and the curvilinear angle.

In the plane, the curve triangle's angle's summation may be bigger than or be smaller than π.

The surface may also be parallel mutually.The concentric spherical surface is mutually parallel.

The spherical surface is in the space these maintains with the fixed point the parallel distance is the r these spot set.The spherical surface and the center are parallel.

。。。。。。


Second, diagrammatic curve parallel

As shown in Figure 2:

In the plane, the rectangular two red side is parallel,

If we cause the rectangle to turn the cylinder, then that two red side is not parallel? I think them parallel, because between them the distance is constant.

If we cause the circular cylinder to turn the frustum, then that two red side is not parallel? I think them parallel, because between them the distance is constant.

If we cause the frustum to press the plane, then that two red side is not parallel? I think them parallel, because between them the distance is constant. (the attention, that two red side was precisely a concentric circle by now! ).

Therefore, once we acknowledge the straight line to be possible mutually parallel, then we can also not but acknowledge the curve also to be possible mutually parallel! The Euclid geometry only realized straight line parallel, but has neglected curve being parallel. He has received the historical limitation.

What is the parallel essence? This is the distance maintains constant invariable! No matter but whether is the straight line!



Third, about the non-Euclid geometry (including spherical geometry)

The spherical geometry thought that in the spherical surface does not have the parallel line. Actually this view is correct, is also wrong. In the spherical surface does not have the straight parallel line, but in the spherical surface actually has the curving parallel line. For instance, in the spherical surface latitude parallel is mutually parallel. Measures the grounding not mutually parallel, but this was not equal to said that in the spherical surface other curves may not be mutually parallel.

In the plane, through a known straight line's outside spot, has a straight line and the known straight line parallel, this is correct. In the spherical surface, through a known curve's outside spot, has a curve and the known curve parallel, this is also correct. Therefore may not remove the axiom of parallels in the spherical geometry! Certainly may not remove the axiom of parallels in the hyperbolic geometry!

The non-Euclid geometry thought: Crosses a straight line spot to be possible to make two straight lines and the known straight line at least parallel, actually this is the idea has the question. First, this confused has been parallel with the concept which did not intersect, because did not intersect was not equal to that was parallel, (in the Euclid geometry, because was parallel is limited in straight line, but in straight line, did not intersect as if is parallel, but in curve, did not intersect not necessarily is parallel); Second, this has confused the straight line and the curve difference, because the non-Euclid geometry said the straight line is a curve in fact!




Fourth, about absolute geometry

After the above revision, three geometries will unify completely and fuse one to be overall, humanity's geometry henceforth only will then perhaps become the absolute geometry.

 

[phya]

https://www.physicsforums.com/attachment.php?attachmentid=28468&d=1285242201"

 

[HallsofIvy]

I asked you, 42 posts ago, to state what definition of "parallel" you are using. Since you have refused to do so, I don't see how anyone can say anything sensible about your statements.

 

[phya]

I asked you, 42 posts ago, to state what definition of "parallel" you are using. Since you have refused to do so, I don't see how anyone can say anything sensible about your statements.

Parallel is the distance maintains invariable, for example, between the distance maintains invariable, between the curve the distance maintains invariable, between the surface the distance maintains invariable and so on.

 

[G037H3]

Concentric circles are an example of parallel curves.

 

[Mentallic]

You can see concentric circles as being parallel from the perspective of the centre of each circle (the distance from the first to the second circle is constant, as measured from the centre) but from another viewpoint (say, and observer looking towards both circles) then they are suddenly not following this rule.

From the centre of the circles viewpoint, this says in coordinate geometry that x^2+y^2=r^2 is "parallel" to x^2+y^2=R^2

but from the observer which is found situated far along the y-axis (as to observe both circles head on) then he will see two circles as "parallel" if they are of the form
x^2+y^2=r^2 and x^2+(y-c)^2=r^2

Now one property of parallel lines is that if line A is parallel to line B and line A is parallel to line C then B is parallel to C. Following this rule, this would mean that x^2+y^2=R^2 is "parallel" to x^2+(y-c)^2=r^2 ? This is why we give concentric circles a description other than "parallel". And we should keep it that way to avoid ambiguity.

 

[phya]

concentric circles are an example of parallel curves.

yes!

 

[phya]

You can see concentric circles as being parallel from the perspective of the centre of each circle (the distance from the first to the second circle is constant, as measured from the centre) but from another viewpoint (say, and observer looking towards both circles) then they are suddenly not following this rule.

From the centre of the circles viewpoint, this says in coordinate geometry that x^2+y^2=r^2 is "parallel" to x^2+y^2=R^2

but from the observer which is found situated far along the y-axis (as to observe both circles head on) then he will see two circles as "parallel" if they are of the form
x^2+y^2=r^2 and x^2+(y-c)^2=r^2

Now one property of parallel lines is that if line A is parallel to line B and line A is parallel to line C then B is parallel to C. Following this rule, this would mean that x^2+y^2=R^2 is "parallel" to x^2+(y-c)^2=r^2 ? This is why we give concentric circles a description other than "parallel". And we should keep it that way to avoid ambiguity.

Your understanding is not necessarily correct, like the chart shows, the left side two circles are parallel, but the right side two circles are not parallel. Why? Because the circle and the circle distance is dissimilar. The attention, I said am the center of circle and the center of circle distance.