Momentum calculation of a rotating rod

[liuxinhua]

$\ \ \ \ \$Calculate the 4 momentum of a rotating rod. We divide it into 4 parts. The part 1 is the work of predecessors.
$\ \ \ \ \$In Special relativity, the motion of rod AB (which is an object in non inertial motion) can be described in an inertial reference frame and the motion of rod AB can be converted to be described in another inertial reference system, by Lorenz transformation.
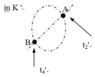
$\ \ \ \ \$In inertial reference frame $K$, an isolated rod AB rotates around its mid point O at uniform angular velocityω, keeps the linear state.
$\ \ \ \ \$For each point on AB, the distance from point O to this point measured in$K$is constant; denote it is$r$. Such as for point D，$r_D$is a constant. For each point on OA, its equation of motion is$x=r\cos(ωt)$, $y=r\sin(ωt)$ . For each point on OB, its equation of motion is$x=r\cos(ωt+π)$, $y=r\sin(ωt+π)$.
$\ \ \ \ \$The inertial reference frame $K’$ moves relative to $K$at speed$v$. Relative to$K’$, the auxiliary circle D and M appear as ellipses D and M, and they move at speed$-v$.
$\ \ \ \ \$Relative to$K’$, rod AB can't keep the linear state at all times. The shape of rotating wheel relative to $K’$ has been studied by the follow reference.
[1] A relativistic trolley paradox, Vadim N. Matvejev, Oleg V. Matvejev, and Ø. Grøn, American Journal of Physics 84, 419 (2016).
[2] A Rotating Disk in Translation, http://www.mathpages.com/home/kmath197/kmath197.htm.
[3] Appearance of a Relativistically Rotating Disk, Keith MeFarlane, International Journal of Theoretical Physics, Vol.20. No.6, 1981.

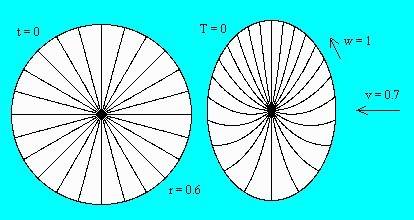
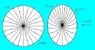
Fig.8. The non-rotating disk is drawn to the left and the rolling disk to the right. Radial lines of the rolling disk are curved as observed by simultaneity in the frame$K’$

$\ \ \ \ \$They have considered a wheel or a disk. Now we consider the momentum of a spokes on the wheel.
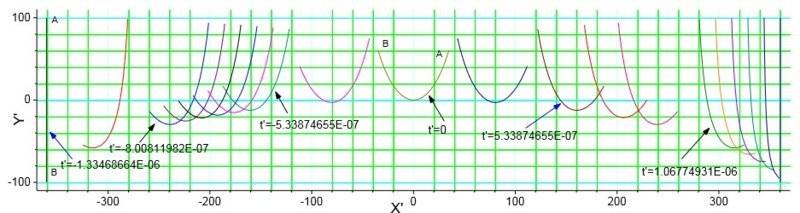
$\ \ \ \ \$With parameter$r_A=100m$, $ω=-2.7E6rad/s$,$v=-0.9c$, using numerical methods, get the shape of AB observed in $K’$.

 

[liuxinhua]

$\ \ \ \ \$ In $K’$, at time$t_1’$=0, an event occurs at the coordinate of point $D( x_{D1}’, y_{D1}’ , 0 , t_1 ’ )$; another event occurs at the coordinate of point $E( x_{E1}’, y_{E1}’ , 0 , t_1 ’ )$. Using Lorentz transformation between two inertial frames, get the two events occurs at $( x_{D t_{D\ one }}, y_{D t_{D\ one }}, 0 , t_ {D\ one } )$, and $( x_{E t_{E\ one }}, y_{E t_{E\ one }} , 0 , t_ {E\ one } )$ in$K$. $t_ {D\ one }≠ t_ {E\ one }$.

$\ \ \ \ \$When $r_A=10m$, $ω=2.4E7rad/s$, $v=0.8c$, $r_D=r_E=6m$. The approximate values by the numerical calculation are as follows:
$\ \ \ \ \$$D( x_{D1}’, y_{D1}’ , 0 , t_1 ’ )$is (3.3699, 2.110599,0, 6.46E-16).
$\ \ \ \ \$$E( x_{E1}’, y_{E1}’ , 0 , t_1 ’ )$is (-3.3699, 2.110599,0, -6.46E-16).
$\ \ \ \ \$$( x_{D t_{D\ one }}, y_{D t_{D\ one }}, 0 , t_ {D\ one } )$is (5.616526, 2.110599,0,1.497740E-08) .
$\ \ \ \ \$$( x_{E t_{E\ one }}, y_{E t_{E\ one }} , 0 , t_ {E\ one } )$ is (-5.616526, 2.110599,0,-1.497740E-08).

$\ \ \ \ \$Set $ω$>0, $v=ωr_A <c$.
$\ \ \ \ \$The shape of AB at the two giving moment is roughly like the lower figure, observed in$K’$.

 

[pervect]

$\ \ \ \ \$Calculate the 4 momentum of a rotating rod.
...
Now we consider the momentum of a spokes on the wheel.
$\ \ \ \ \$With parameter$r_A=100m$, $ω=-2.7E6rad/s$,$v=-0.9c$, using numerical methods, get the shape of AB observed in $K’$. View attachment 229431

I see no mention of you computing the stresses in the rod, though I see some talk about a "numerical computation", I don't know what formula you used to do said computations. I'd assume they're based on point masses and don't use tensor methods, however.

WIthout including the stresses in the rod, any answer will only be an approximation to the full relativistic answer Energy, momentum, and stress are all part of a larger relativistic object, the stress-energy tensor. Without including all the terms of the stress energy tensor (specifically the stres terms) in the calculation, I don't believe you'll get a totally self-consistent relativistic answer. If the rod is rotating slowly enough where the stresses are small, one might get an approximate answer, it's unclear exactly when/how the approximation breaks down without further analysis, however.

The particles composing the rod are not isolated, they are interacting via forces. Hence all the previous cautions about non-isolated systems apply.

I'm not sure exactly what the goal is, if the rod is rotating around the midpoint, the total momentum is obviously zero by symmetry. This leaves the computation of the energy of the rod rotating around it's midpoint, and the angular momentum of the rod as the interesting physical quantities.

My general reaction is that the fundamental approach needs revision, you won't get a meaningful answer with a point-particle based approach. You really need to learn about the stress-energy tensor to solve this sort of problem.

Egan has dome some work on the relativsitic rotating hoop that illustrate a valid approach to a similar problem, though it's not peer-reviewed. http://www.gregegan.net/SCIENCE/Rings/Rings.html

 

[liuxinhua]

$\ \ \ \ \$ In this part, it is mainly about the work of predecessors.
$\ \ \ \ \$The shape of a rotating rod in different inertial reference frames.
$\ \ \ \ \$In this section, only consider the shape of rods in different inertial reference frames. It does not involve the distribution of quality and tension.

$\ \ \ \ \$In $K$, an isolated rod AB rotates around its mid point O at uniform angular velocity $ω$, keeps the linear state.
$\ \ \ \ \$In $K$, the shape of the rod is determined by its motion equation.
$\ \ \ \ \$By using Lorenz transform between $K$ and $K’$, we get the shape of the rod in $K’$.
$\ \ \ \ \$For example, if we want to get the shape of the rod at time $t_1’$ in $K’$. For each point on AB, such as point D on OA, Solving equations
$\ \ \ \ \$$t_1’=γ (t- \frac v {c^2} x)$
$\ \ \ \ \$$x= r_D \cos(ωt)$
$\ \ \ \ \$$γ= \frac 1 {\sqrt {1- \frac {v^2} {c^2} }}$
$\ \ \ \ \$Then use the solutions $x$ and $t$ to get the position of D at time $t_1’$ in $K’$，by using Lorenz transform between $K$ and $K’$.
$\ \ \ \ \$Here, we do not touch the tension of rods.

$\ \ \ \ \$In subsequent work, we did not calculate the specific value of the rod tension.
$\ \ \ \ \$But there is a fact that measured in $K$ the tension at each position on the rod does not change with time.
$\ \ \ \ \$Rod AB is an isolate system, but section DM and EN isn’t isolate systems.
$\ \ \ \ \$In order to calculate the momentum of section DM and EN, it is necessary to cut them into infinitely small segments and calculate the rest mass and velocity of each segment.
$\ \ \ \ \$We consider the sum rest masses of a confirmed segment in $K’$ is equal to its value when measured in $K$, no matter whether it is stretched or not, so long as its stretching degree remains unchanged measured in $K$.

$\ \ \ \ \$And we consider: A rod is static in an inertial reference system. When the rod is free, it has a rest mass. When the rod is stretched, it has another rest mass. The rest mass of the rod when it is stretched is greater than the rest mass of the rod when it is free. When the rod is static at different states such as free or stretched, the potential energy of the particles is different.

$\ \ \ \ \$Thank the help of @pervect. I really need help.

 

[pervect]

$\ \ \ \ \$ In this part, it is mainly about the work of predecessors.
$\ \ \ \ \$The shape of a rotating rod in different inertial reference frames.
$\ \ \ \ \$In this section, only consider the shape of rods in different inertial reference frames. It does not involve the distribution of quality and tension.
$\ \ \ \ \$In $K$, an isolated rod AB rotates around its mid point O at uniform angular velocity $ω$, keeps the linear state.
$\ \ \ \ \$In $K$, the shape of the rod is determined by its motion equation.
$\ \ \ \ \$By using Lorenz transform between $K$ and $K’$, we get the shape of the rod in $K’$.
$\ \ \ \ \$For example, if we want to get the shape of the rod at time $t_1’$ in $K’$. For each point on AB, such as point D on OA, Solving equations
$\ \ \ \ \$$t_1’=γ (t- \frac v {c^2} x)$
$\ \ \ \ \$$x= r_D \cos(ωt)$
$\ \ \ \ \$$γ= \frac 1 {\sqrt {1- \frac {v^2} {c^2} }}$

OK, I agree with that. K is the inertial rest frame of the center of the rod, K' is moving with some velocity v with respect to K, and the rod bends and changes length in K' given that the notion of the shape of the rod is defined by it's shape at some particular instant in time in K' using the simultaneity conventions in K'.

I did work this out once, though I couldn't find the relevant post. Eyeballing your approach, it looks like you're doing fine as far as describing the shape of the rod in K'.

$\ \ \ \ \$Then use the solutions $x$ and $t$ to get the position of D at time $t_1’$ in $K’$，by using Lorenz transform between $K$ and $K’$.
$\ \ \ \ \$Here, we do not touch the tension of rods.

$\ \ \ \ \$In subsequent work, we did not calculate the specific value of the rod tension.
$\ \ \ \ \$But there is a fact that measured in $K$ the tension at each position on the rod does not change with time.

Yes. There is a way to find the tension in K knowing the tension, density, and momentum in K', and vica-versa, but it involves using tensors and tensor methods that are usually taught in GR. Mostly one is not interested in the tension in K, one is interested in the energy and momentum density in K. But the energy and momentum density in K is different than the energy and momentum in K', it needs to be transformed. The topic of how to do this involves the topic of describing tension, density, and momentum density as a tensor, and then describing how this tensor transforms by knowing how tensors in general transform when one changes coordinates.

$\ \ \ \ \$Rod AB is an isolate system, but section DM and EN isn’t isolate systems.
$\ \ \ \ \$In order to calculate the momentum of section DM and EN, it is necessary to cut them into infinitely small segments and calculate the rest mass and velocity of each segment.

But there's more to it than that. The momentum (density) of the non-isolated section of the rod in K depends not only on the momentum (density) in K', but the tension in K' and the density in K'. One cannot transform the energy momentum 4-vector via the Lorentz transform, one needs to write the rank 2 tensor, the stress-energy tensor, and transform that. Then one can pick out the components of the transformed tensor that represent momentum (or anything else one wants to know) in whatever frame one wants to know them in.

When you package all the necessary components (energy density, momentum density, and the various pressure and tension terms) into one tensor, you have the information you need to compute all these quantites in another frame. But you need to know all the quantities, not just some of them, to do a correct transformation.

I'm not aware of any way of formulating the problem correctly that doesn't use the stress energy tensor.

 

[SlowThinker]

@liuxinhua It's not clear where you're going but it has been established many times in very long discussions that analyzing rotating objects in frames where the center is moving never leads to anything useful.

In particular, the center of mass may not move in a straight line, and the angular momentum is not conserved throughout the period of rotation.
If you're going to re-discover these, I just wanted to say it's nothing new.

 

[liuxinhua]

Please help me to find out the mistake.
I get a wrong result in part 4 https://www.physicsforums.com/threads/momentum-calculation-of-a-rotating-rod-part-4.953636/,but I can't find where is the mistake.

@liuxinhua It's not clear where you're going but it has been established many times in very long discussions that analyzing rotating objects in frames where the center is moving never leads to anything useful.

In particular, the center of mass may not move in a straight line, and the angular momentum is not conserved throughout the period of rotation.
If you're going to re-discover these, I just wanted to say it's nothing new.

 

[liuxinhua]

Answer to Mentor.
Mentor said: My suggestion therefore is, that you try and find a way to specifically ask one question about some lines and not: Here is my long essay, find the error!

I put my thoughts on this purpose for the following questions:
1, Is it possible to study a born rigid body with a non inertial motion in the special relativity?
In my opinion, the born rigid body constitutes a non-inertial reference frame. but as long as we use the Lorentz transformation, only use the parameters measured in the inertial reference frame, and not include any parameters from the non-inertial reference frame, there will be no problem.

2, Is the sum of the rest masses of a born rigid body a constant, relative to any inertial reference frame?
Pallen has already answered this question. Thank very much to Pallen.

3, Is my calculations based on false premises?

4, If my mind is chaotic, when I think about the content of my post, I hope someone can help me to correct my thinking mode.


I submit the content of my post to a SCI magazine, below is the letter from the magazine.

The paper consider an isolated rod rotating with uniform angular velocity and two inertial reference systems, one of them in which the rod is seen to uniformely rotate around its center of mass, and the other moving relative to the first one at speed v. Using the Lorentz coordinate transformation formula between two inertial reference systems the author concludes that four-momentum vector is not conserved.

However, a rotating rod is actually an accelerating system so its frame is not inertial and the Lorentz transformations only refers to coordinate transformations between inertial frames. What remains is an extremely confused presentation consisting of repetetive phrases and calculations based on false premises.

 

[PAllen]

I am not planning to read through your pages of calculations, but I make the following statements of what should be the result, and offer a suggestion that I hope will go a long way to helping you find your problem.

1) You should find that that in both frames (call them K and K'), total 4-momentum is constant over time.
2) In K, the total 4 momentum will be (E,0), where E is the total energy (rest plus kinetic) of all elements, accumulated. In K', you should find (γE,-γEv) as the total 4 momentum, with v being the speed of K' relative to K, and γ as the standard function of v. I use convention of c=1, so E is also the invariant mass.

If this is not what you get from your calculation, then it is wrong and a good way to localize this is a drastic simplification. I suggest considering two co-revolving particles (on opposite sides of a circle), each of mass m, in K. The total 4-momentum in K is obviously (2γ(rω)m,0). Using the same methods you use for rod elements, compute total 4-momentum in K'. If you get something different from (2γ(v)γ(rω)m,-2γ(v)γ(rω)mv), then it should be much easier to find your error in this simple case. If this case works by your methods, then it must be something about the way you go to the continuum and integrate that is your problem. Perhaps replace two point masses with two small rod elements, and see if you can get that to work right.

 

[PeterDonis]

Is it possible to study a born rigid body with a non inertial motion in the special relativity?

Yes. But you seem to be equating "special relativity" with "inertial reference frame". They're not the same.

In my opinion, the born rigid body constitutes a non-inertial reference frame.

Yes. For example, look up "Rindler coordinates"; the individual points of a body undergoing Born rigid acceleration are at rest in Rindler coordinates.

as long as we use the Lorentz transformation, only use the parameters measured in the inertial reference frame, and not include any parameters from the non-inertial reference frame, there will be no problem.

You can do the analysis this way, yes. You can also do it by using a suitable non-inertial frame (such as Rindler coordinates for the case described above). Both should give the same answers if you've done them correctly.

 

[liuxinhua]

Consider two co-revolving particles (on opposite sides of a circle), each of rest mass $m_0$, in $K$.
Assume, the centre of the two particles is a fixed point in $K$.
The total 4-momentum $P(t)$ is $(2γ(rω)m_0,0,0,0)$ in $K$.
But the total 4-momentum of the two particles $P(t')$ in $K'$ isn’t always equal to a constant.

At time ${t_3}'$, $P({t_3}')$ is $(2γ(v)γ(rω)m_0,-2γ(v)γ(rω)m_0 v, 0,0)$.

At time ${t_2}'$, $P({t_2}')$ is $(2γ(v)γ(rω)m_0, γ(v)γ(rω)m_0 (u_{A \ two \ x}-v) +γ(v)γ(rω)m_0 (u_{B \ two \ x} -v), \ \ \ ,0)$. $P({t_2}')$ is not $( 2γ(v)γ(rω)m_0, γ(v)γ(rω)m_0 (u_{A \ two \ x}-v) +γ(v)γ(rω)m_0 (u_{B \ four\ x} -v) ,\ \ \ ,0)$.

The 4-momentum of particle $A$ in $K'$ at time ${t_2}'$ and The 4-momentum of particle $B$ in $K'$ at time ${t_4}'$, $P(A,{t_2}')$+ $P(B,{t_4}')$, is $(2γ(v)γ(rω)m_0,γ(v)γ(rω)m_0 (u_{A \ two \ x}-v)+γ(v)γ(rω)m_0 (u_{B \ four\ x} -v) , \ \ \ ,0)$, which is equal to $(2γ(v)γ(rω)m_0,-2γ(v)γ(rω)m_0 v, 0,0)$.

Because the two particles is not an isolated system, this is not contradictory to conservation of momentum.

$\ \ \ \ \ \$

I am very glad. I have found the channel that I can communicate with you effective.

My calculation in part3 is to get ${γ(t’,l’) }’ {u_{x}{(t’,l’) }}’$.
$γ_ {D} ({ t}’) ’ u_ {Dx} ({ t}’) ’$, which has a expression at post #15.
Through your message, I can write it as $γ_ {D} ({ t}’) ’ u_ {Dx} ({ t}’) ’$=${ (u_ {Dx} ( t) –v) γ(v)γ(r_ {D}ω)}$=${(-r_D ω \sin(ωt_{D\ one }) –v) γ(v)γ(r_ {D}ω)}$.
Through your post #18, it is correct.

And at condition:
$\ \ \ \ \$Set time ${t_1}’=0$ in $K’$.
$\ \ \ \ \$Set time $t_{three}=\frac π {2ω}$ in $K$.
$\ \ \ \ \$Set $ω>0$, $c>v=ωr_A>0$.

$\ \ \ \ \$For point on OA,${γ_α(t’,l’) }’ {u_{αx}{(t’,l’) }}’$=$( {-r ω \ sin(ωt_α(t’,r)) -v} ) γ(v)γ(rω)$
$\ \ \ \ \$$\ \ \ \ \$$\ sin(ωt_α({t_1}’ , r))>0$
$\ \ \ \ \$$\ \ \ \ \$$\ sin (ω t_α({ t_3}’ , r))=1$

$\ \ \ \ \$For point on OB,${γ_ β (t’,l’) }’ {u_ {βx} {(t’,l’) }}’$ = $({-r ω \ sin(ωt_β(t’,r) +π) -v}) γ(v)γ(rω)$
$\ \ \ \ \$$\ \ \ \ \$$\ sin(ωt_β({t_1}’ , r) +π)>0$
$\ \ \ \ \$$\ \ \ \ \$$\ sin (ω t_β({ t_3}’ , r) + π)=-1$

In fact, all my statements in post #15 are for two purposes.
One is: the relationship of ${t_1}’$ and $t_{D\ one }, t_{E\ one }$; the relationship of ${t_3}’$ and $t_3$, for Relativity of simultaneity.
Another one is: when ${t_1}’=0$, the $y$ coordinates of rod $AB$ except point $O$ are greater than 0; when ${t_3}’$, the $x$ coordinates of rod $AB$ are equal to each.

I am not planning to read through your pages of calculations, but I make the following statements of what should be the result, and offer a suggestion that I hope will go a long way to helping you find your problem.

1) You should find that that in both frames (call them K and K'), total 4-momentum is constant over time.
2) In K, the total 4 momentum will be (E,0), where E is the total energy (rest plus kinetic) of all elements, accumulated. In K', you should find (γE,-γEv) as the total 4 momentum, with v being the speed of K' relative to K, and γ as the standard function of v. I use convention of c=1, so E is also the invariant mass.

If this is not what you get from your calculation, then it is wrong and a good way to localize this is a drastic simplification. I suggest considering two co-revolving particles (on opposite sides of a circle), each of mass m, in K. The total 4-momentum in K is obviously (2γ(rω)m,0). Using the same methods you use for rod elements, compute total 4-momentum in K'. If you get something different from (2γ(v)γ(rω)m,-2γ(v)γ(rω)mv), then it should be much easier to find your error in this simple case. If this case works by your methods, then it must be something about the way you go to the continuum and integrate that is your problem. Perhaps replace two point masses with two small rod elements, and see if you can get that to work right.

I found I have done a wrong decision.

This is the reason that my knowledge is too narrow.
Now I will use $γ_ {D} ({ t}’) ’ u_ {Dx} ({ t}’) ’$=${ (u_ {Dx} ( t) –v) γ(v)γ(r_ {D}ω)}$=${(-r_D ω \sin(ωt_{D\ one }) –v) γ(v)γ(r_ {D}ω)}$ again.

 

[liuxinhua]

1, Is it possible to study a born rigid body with a non inertial motion in the special relativity?
I mean: In the special relativity, "In an inertial reference frame we can decribe the motion of a born rigid body with a non inertial motion. Then, we can use the Lorentz transformation, get the motion of the born rigid body in another inertial reference frame." is right ?

Yes. But you seem to be equating "special relativity" with "inertial reference frame". They're not the same.

 

[fresh_42]

On the question about premises:

I think, what he referred to as "my premise" is:
$\ \ \ \ \$ In $K$, an isolated rod AB rotates around its mid point O at uniform angular velocity $ω$, keeps the linear state. For each point on AB, the distance from point O to this point measured in $K$ is constant; denote it is $r$. Such as for point D，$r_D$ is a constant. For each point on OA, its equation of motion is $x=r\cos(ωt)$, $y=r\sin(ωt)$ . For each point on OB, its equation of motion is $x=r\cos(ωt+π)$, $y=r\sin(ωt+π)$. Rod AB is a Born rigid body.
$\ \ \ \ \$ For actual rod AB, there is micro motion on molecular level. In the process of simplifying and establishing a mathematical model, we do not consider this micro motion. The rod AB is an ideal system without any relative movement between the components relative to $K$. The distribution of material and potential energy on the rod AB along the length is symmetry about mid point O and it does not change with time, measured in $K$. Rod AB has no thickness along $θ$ direction, if transform $K$ from rectangular coordinate system to polar coordinate system. That is to say consider rod AB as a one-dimensional rod on $x-y$ plane relative to$K$.

$\ \ \ \ \$That is : Rod $AB$ is a one-dimensional born rigid body. Although it is stretched, the degree of stretching in each position may be different, but the degree of stretching in each position is no longer changed.Rod $AB$ keeps the linear state in $K$.

 

[PAllen]

@liuxinhua 's finding is quite interesting to me. In the case of two co-revolving masses, I agree with his calculation that even though momentum is exactly conserved in the COM frame, it is not conserved (specifically, it oscillates around an average value) in a different inertial frame. This says there is much subtlety to the notion of closed system that conserves momentum in all inertial frames. It is not necessarily enough to conserve momentum in one frame 'by accident'.

I think the issue gets to the requirement that SR consistent dynamics must be strictly local, with local conservation. In my oversimplified co-revolving masses, there is nothing locally causing their momentum change. If you, for example, treat them as oppositely charged particles, then they have local interaction with the EM field, whose momentum and energy must be accounted for (and, of course, it is well known that the system cannot be stable, classically, due to generated EM radiation).

So my simplification went too far. There may be no simpler case expected to work than what @liuxinhua is trying: a continuous 1-d rod, treated as a Hookean 1-d spring, in an equlibrium rotating state. It may even be necessary that tension must be explicitly accounted for. The transformation properties of the stress energy tensor (SET) are as a tensor, so that tension and other components of the tensor (e.g. energy density) can exchange places in different frames, just as space and time mix between frames. If there is really no error in the OP's analysis of the rotating rod, then the implication is that you cannot ignore the correct treatment of tension if you want a consistent behavior in relativity, with conservation in all frames.

 

[PeterDonis]

I mean: In the special relativity, "In an inertial reference frame we can decribe the motion of a born rigid body with a non inertial motion. Then, we can use the Lorentz transformation, get the motion of the born rigid body in another inertial reference frame." is right ?

Yes, you can always Lorentz transform quantities between inertial frames. But, as I said, "special relativity" is not restricted to inertial frames. The key restriction of special relativity is that spacetime has to be flat.

 

[liuxinhua]

Yes, you can always Lorentz transform quantities between inertial frames. But, as I said, "special relativity" is not restricted to inertial frames. The key restriction of special relativity is that spacetime has to be flat.

I understand what you mean is: $K$, must be an inertial space.

$K$, it is originally a flat space.
But when I put a rotating rod in it, it will not be a flat space.
In this sense, there is no flat space and no inertial reference frame.
We only can do this: Reduce the mass of the rod AB to one half of the original mass, and then to one half of the mass just now, until infinitesimal, in $K$. And the velocity of $K’$ relative to $K$ is not infinitely close to $c$. (or $\frac v c$ is not infinitely close to 1)

.
In fact, we only know there is rest mass (include potential energy) of rod AB, but we have not set a specific value to it.
In this way, we think when we put a rotating rod in space, the space is still flat.

 

[liuxinhua]

@PAllen, Two identical objects $A$ and $B$ rest in $K$, before time $t_0$:

They have the same sum rest masses.

One of them ($B$) is deformed under external force, from time $t_0$ to $t_9$:

After time $t_9$, they don’t have the same sum rest masses.
In fact, we consider the internal tension or internal potential energy as rest mass.

When we calculate the change of momentum of objects $B$ in $K’$, we have two ways.
One is: Calculate the external force act on objects $B$ in $K’$, and integrate it. When calculate the external force act on objects $B$ in $K’$ , we need to use tension.

The other one is: Calculate the momentum of objects $B$ in $K’$ at time($t_{0}’$) before its deformation and at time ($t_{9}’$) after its deformation. Then compare these two values. If we can get the rest mass of objects $B$, we don’t need to calculate the tension and the external force.

So, for the rotating bar, we do not need to know the specific value of its internal tension, nor do we need to know what laws its tension and deformation obey, as long as we know that it is a born rigid body. A born rigid body with internal tension.

So, for the rotating bar, we have know its rest mass line density along the rod. We do not need to know the specific value of its internal tension, nor do we need to know what laws its tension and deformation obey, as long as we know that it is a born rigid body. A born rigid body with internal tension.

 

[liuxinhua]

I think I still need to post Part 2.
Part 2 The relationship of the rest mass line density along AB between$K$ and $K’$

$\ \ \ \ \$The follow-up description is based on the premises on post #13.

$\ \ \ \ \$$r$ represents the position of a point on AB, and $r$ is a constant for each confirmed point.

$\ \ \ \ \$In $K$, for each position on AB, denote $ρ (r)$ as the rest mass line density at the position, $r$ is the distance from point O to this position. $ρ (r)$ is equal to the rest mass of the segment at position $r$ on AB divided by the length of this segment (the length of this segment need to be infinitesimal).

$\ \ \ \ \$In $K’$, at time $t’$, for each point on OA, denote $l’$as the curve length from point O to this point along curve OA. $l’$=$f_α (t’,r)’$. For example, at the moment ${t_1}’$, the length of the curve OD is $l_D ({t_1}’)’$=$f_α ({t_1}’,r_D)’$. denote $ρ_α(t’,l’) ’$ as the rest mass line density at the position when the curve length from point O to this position is $l’$ measured in $K’$ at the time $t’$. $ρ_α(t’,l’) ’$= $ρ_α(t’, f_α ({t}’,r)’ ) ’$. Remember $g_α ({t}’,r)’= ρ_α(t’, f_α ({t}’,r)’ ) ’$.

$\ \ \ \ \$Rod AB is a Born rigid body.
$\ \ \ \ \$$m_{sum\ 0 \ OD } ={m_{sum\ 0 \ OD } ({t}’ )} ’$
$\ \ \ \ \$$m_{sum\ 0 \ OD }$=$\int_{0} ^{ r_D } {ρ (r)} \, dr$
$\ \ \ \ \$${m_{sum\ 0 \ OD } ({t}’)} ’ = \int_{ 0} ^{ l_D(t’) } {ρ_α({t}’,l’) ’} \, dl’$ , and $l’ = f_α ({t}’,r)’$. Make variable substitution for the integral $l’ →r$,

$\ \ \ \ \$${m_{sum\ 0 \ OD } ({t}’) } ’ =\int_{ 0} ^{ r_D } {ρ_α({t}’, f_α ({t}’,r)’) ’ \frac {\partial f_α ({t}’,r)’} {\partial r}} \, dr$ =$\int_{ 0} ^{ r_D } {g_α({t}’, r) ’ \frac {\partial f_α ({t}’,r)’} {\partial r}} \, dr$

$\ \ \ \ \$So, $\int_{ 0} ^{ r_D } {g_α({t}’, r) ’ \frac {\partial f_α ({t}’,r)’} {\partial r}} \, dr$=$\int_{ 0} ^{ r_D } ρ(r) dr$, and because of the arbitrariness of the auxiliary circle D, there is

$\ \ \ \ \$ For each position on OA, ${g_α({t}’, r) ’ \frac {\partial f_α ({t}’,r)’} {\partial r}}$=$ρ(r)$

$\ \ \ \ \$The same, for each position on OB, there is ${g_β({t}’, r) ’ \frac {\partial f_β({t}’,r)’} {\partial r}}$=$ρ(r)$

 

[PAllen]

Clearly your (@liuxinhua) example problem is informative in the sense of showing flawed intuitions. Even after years of work with relativity, I occasionally find cases where I assume a Newtonian intuition is still true relativistically. That is the case here. My agreement with your argument that rest mass within a unit element of a born rigid body is frame invariant (even though generally, sum of rest mass is neither conserved nor frame invariant) was based on the intuition there were no local interactions going on. I now argue that this is false. For a treatment of the rotating rod consistent with relativistic dynamics one must involve local interactions that locally conserve 4-momentum up to flows in and out. The components of the rotating rod in equlibrium in the COM frame are undergoing local interactions with its neighbors that balance globally and locally in this frame, and you can get away with ignoring them. However, in a different inertial frame, the distances between elements of the rod are dynamically changing (periodically), and the magnitudes (as well as direction) of their 4-momenta are changing (again, periodically). A momentum conserving description in this non-COM frame must account for the local dynamics. I think part of the resolution involves that tension is not a relativistic scalar, but instead is a component of a tensor. It is not a frame invariant quantity. Thus, in a frame where the rod elements are locally undergoing dynamic changes (as described above), the tension within a rod element may not be constant as expressed in this non-COM frame, and neither will the rest mass of the element. Even though its hypothetical particles will not change rest mass, the contribution of potential energy to a unit's rest mass will not be constant in this non-COM frame.

Thus, the minimum complexity needed for relativistic consistency must involve a dynamical 1-d spring model, including potential energy, if you want to analyze it in a non-COM frame. The equilibrium cancellations simply do not happen in the non-COM frame.

 

[pervect]

My take on the problem is somewhat similar to Pallen's. The rod is manifestly rigid in the center of mass frame, but this rigidity is not manifest in any other frame. The symmetries in the equations still exist, but the choice of coordinates (in particular, the choice of simultaneity convention of a moving frame) obscures the symmetries, making the problem more difficult to solve, without actually changing the solution.

PAllen notes the need for a dynamic model of a 1-d spring. This is, in my opinion, basically a step towards modelling the bar via partial differential equations. An infinite array of 1-d "spring + mass" systems is a well-known technique for gaining some intuition about the limiting case where there are lots of springs and lots of masses. The technique of many 1d "spring + mass" systems to model a physical system is also useful numerically, I believe I've seen it referred to as "finite element analysis". The mathematical limit of this approach is the well-known approach of partial differential equations, henceforth PDE's.

I also like to talk about this problem in terms of PDE's, because it's not too clear how to model a relativistic spring for the spring-mass approach. Abstracting the problem to PDE's avoids this issue.

One might not have the intuition developed for partial differential equations that one does for ordinary differential equations (I know I don't), but they're not terribly exotic either. If an object is changing shape, due to dynamic effects, this is the approach that comes to mind to model it.

Tensor techniques work very well with the PDE's, but I suppose they may not be essential, though tensor techniques are how I would approach the problem.

The distributed rod can be modeled in any frame of reference by PDE's. The technique of using PDE's is the "obvious" technique one would use for a dynamic mechanical system that is changing shape. A oversimplifed observation is that in the non-COM frame, the rod is changing shape. Therefore one "needs" (shorthand for - I don't know any better way of doing it that will get the correct answer) to use techniques that can handle objects that are dynamically changing their shape to perform the analysis in the non-COM frame. The techniques for doing this are well-known, though they may not be intuitive. They are the techniques of using PDE's to model the rod.

Usually PDE's are introduced for electormagnetism. At the graduate level, the PDE"s of electromagnetism are used to motivate tensor techniques, for instance Jackson's "Classical Electrodynamics".

Once one knows how to model a rod (or any other dynamical mechanical system) with PDE's, one can start to think about the issues of how the PDE's transform when one changes coordinates (or frames of reference). All such changes at the mathematical level are "changes of variables". At a basic level, this isn't any huge mystery. One can simply use algebra to change variables, though there are more systematic approaches to this problem.

It's easy to say "model the rod with PDE's", but it's harder to do. It's probably the topic of an advanced course in mechanical engineering to actually go through all the details. But that's the approach that's "needed" here. (Again by "needed", I mean that it's the easiest way I know of that works.).

 

[liuxinhua]

Numerical calculation can only be considered as a checking method. @pervect
So we must prove it logically.

Whatever the final result, I would like to emphasize that a property of a born rigid body: if an object is a born rigid body in an inertial reference frame; then it is a born rigid body, in any inertial reference frame.

@PAllen, We comeback to the key problem: for one part on a born rigid body (3-dimemsion, we have simplified it to 1-dimension), its sum rest masses is a constant,
$m_{sum\ 0 \ OD } ={m_{sum\ 0 \ OD } ({t}’ )} ’$ may be wrong. I will accept this first.
In $K’$ for OD potential energy is not change over time, but the contribution of potential energy to a unit's rest mass will not be constant in this non-COM frame.

 

[PeterDonis]

if an object is a born rigid body in an inertial reference frame; then it is a born rigid body, in any inertial reference frame.

Actually, it's even stronger than that. Born rigidity is a property of the congruence of worldlines that describes the object in spacetime; it does not depend on any choice of reference frame (inertial or non-inertial).

 

[liuxinhua]

I know I must accept the result: $m_{sum\ 0 \ OD } ={m_{sum\ 0 \ OD } ({t}’ )} ’$ may be wrong. The contribution of potential energy to a unit's rest mass will not be constant in this non-COM frame.

It is not discussed here whether it can be achieved through other channels.
Of course, this can be achieved through other channels.

But, in $K’$, for a confirmed energy, if its potential energy is constant, the contribution of potential energy to it's rest mass is constant?

Potential energy and kinetic energy = $γ(u) m_0 c^2$, kinetic energy=$γ(u) m_0 c^2- m_0 c^2$. Is there potential energy = $γ(u) m_0 c^2-(γ(u) m_0 c^2- m_0 c^2)$= $m_0 c^2$?

Potential energy of a born rigid body is a constant.

How could this happen? The contribution of potential energy of born rigid body to its rest mass will not be constant. I refer to "in any inertial reference frame".

 

[PAllen]

No, I think the potential energy contained in a linear rod 'element' is not constant in K'. In K', you have interchange between potential energy and kinetic energy to account for relative motion between 'particles' in K'. Note that while in K, there is no relative motion because of the simultaneity slicing, the different slicing in K' compares different events along particle world lines, such that there is relative motion. Within K', a consistent description has to provide a local cause for this. An example is conversion of potential to kinetic energy. Thus potential energy varies with time, as does its contribution to rest mass of an element.

Note that the set of events in a rod element in K' are a completely different set of events than in K.

 

[pervect]

Numerical calculation can only be considered as a checking method. @pervect
So we must prove it logically.

I am not advocating numerical methods, except as a motivational tool. Basically, I believe you're not familiar with the techniques I'm describing, and simply pointing out that that these techniqaues will allow you to solve the problem you're interested in doesn't seem to be motivating you to explore these techniques. So I'm trying various other means (mostly unsucessfully, I think) to attempt to motivate you to learn what you need to know so you can answer your own questions.

Specifically, I am advocating the use of partial differential equations to model the relativistic rod, preferably with tensors (but I as looking for ways to simplify the presentation and I believe you could get away without using tensors). I am not specifically the use of numerical methods, though I don't have any objections to numerical methods, personally, if it gets the point across.

Whatever the final result, I would like to emphasize that a property of a born rigid body: if an object is a born rigid body in an inertial reference frame; then it is a born rigid body, in any inertial reference frame.

I suspect you haven't looked at the formal definition of Born rigidity. If you did, you'd see that the Born-rigid rod did indeed meet the required mathematical conditions to satisfy Born rigidity, while at the same time having different shapes at different times as defined by your particular choice of frame. So part of the issue is one of semantics, you are assuming that Born rigidity means one thing, but the actual mathematical formulation is something quite different, something that does not prevent the rod from changing it's shape with time according to a particular time-slicing.

I'd have to dig for what I've seen for the formal definitions of Born rigidity, but as I recall one definition is based on the vanishing of the Lie derivative of the spatial projection of the metric tensor, and the other is based on the vanishing of expansion and shear tensors for a time-like congurence. As Pallen points out, neither defintion requires a choice of frame to carry out (unless one regards a time-like congruence as a sort of frame, I suppose). I would think it would be obvious to you from your reading that the rod can change it's shape with time in the frame where the center of mass moves, you've even quoted references that say it does that. This is not contrary to the idea that the rod is Born rigid, nor that Born rigidity is independent of one's choice of frame, it simply means that the formulation of Born rigidity is more subtle than you appear to think it is.

 

[liuxinhua]

We can’t get “ potential energy between slice will change ” from “there is relative motion between slice” in $K’$.
In $K$, from time $t_1$to time $t_2$， $AB$ accelerating.

In $K’$, there is relative motion between slice. At least at time before acceleration and after acceleration, $AB$ has the same potential energy.
At time before acceleration and after acceleration, $AB$ has the same rest mass.

In my view, the potential energy between molecules is mass，is material.
I have a feeling, that the potential energy of a born rigid body is constant. @PAllen,

I should be a worker; so much information has not been seen by me. @pervect

 

[PAllen]

Here are two papers discussing somewhat related problems that give some notion of the types of things you would need to account for to obtain a consistent description of a rotating rod in different frames.

https://arxiv.org/abs/1205.2823
https://arxiv.org/abs/0712.3891

 

[PAllen]

I suggest an analogy to make frame variance of rest mass of an object without variation of particle number more plausible. Of course, this is just an analogy, and the particles are classical point particles not particles in the QM sense.

Imagine an element of the 1-d rod. It may be treated in spacetime as a world sheet with some number of embedded world lines for the particles. If we slice the world sheet at different angles, we get the same number of world lines, to which we attribute the same mass. However, the length of 'stuff between them' varies with the slicing angle. This 'stuff between them' may be taken to represent energy contributions to rest mass from everything other the particles (be it fields or potential energy). Since the length of this varies by slice (frame), the rest mass of the element can be frame dependent, above and beyond any kinetic contribution of the particles.

Further, in this case, taking the slice orthogonal to the center world line of a rod element as corresponding to the MCIF for this particle, the slices in your actual problem will have a periodic relative angle to this slice (in K'). Thus, periodic change in rest mass of the element should not be surprising.

Sorry that I caused confusion on this. While I argued consistently that summing rest mass is generally useless, I was initially convinced it was a valid simplification in this special case. I now see this is wrong, and the paradoxes you find are evidence of this.

 

[pervect]

I suggest an analogy to make frame variance of rest mass of an object without variation of particle number more plausible. Of course, this is just an analogy, and the particles are classical point particles not particles in the QM sense.

Imagine an element of the 1-d rod. It may be treated in spacetime as a world sheet with some number of embedded world lines for the particles. If we slice the world sheet at different angles, we get the same number of world lines, to which we attribute the same mass. However, the length of 'stuff between them' varies with the slicing angle. This 'stuff between them' may be taken to represent energy contributions to rest mass from everything other the particles (be it fields or potential energy). Since the length of this varies by slice (frame), the rest mass of the element can be frame dependent, above and beyond any kinetic contribution of the particles.

Further, in this case, taking the slice orthogonal to the center world line of a rod element as corresponding to the MCIF for this particle, the slices in your actual problem will have a periodic relative angle to this slice (in K'). Thus, periodic change in rest mass of the element should not be surprising.

Sorry that I caused confusion on this. While I argued consistently that summing rest mass is generally useless, I was initially convinced it was a valid simplification in this special case. I now see this is wrong, and the paradoxes you find are evidence of this.

I've played with the idea of modeling fields as the exchange of particles. Basically, I just imagine that the virtual particles in a QM sense are real, and use these particles to mimic the effects of the fields with an exchange of particles.

To get attractive forces, though, this approach needs negative rest masses. It's strange, but I don't think it hurts anything, and it does give some physical insight into some circumstances, such as explaining why matter with a tension greater than it's density is "exotic matter" and could be used (if it exists) to hold open the throats of wormholes in General relativity.

Object A emits a negative mass particle towards object B, and by the consequence of conservation of momentum it moves towards B, essentialy mimicing an attractive force towards B. Object B reflects the negative mass particle back towards object A, and also experiences a force in the direction towards A by this process.

I think it all makes sense and I think it works out, but I've never seen anything formal written up in the literature about it. I have seen a discussion of the virtual particle model model of attractive forces in one of the sci.physics FAQ's, though. It might be less abstract than trying to introduce the stress-energy tensor. You basically have some real particles that comprise the physical body, and some virtual particles (that you treat as real) that generate the internal stresses in the body.

I have seen "swarms of particles" treatments of the stress-energy tensor in various places, so the idea is perhaps not entirely novel, except for the idea that we can use the swarm-of-particles idea to model the effect of fields without the associated formalisms. I'm not quite to the point where I necessarily want to recommend this approach. But I think it's interesting.

I do feel a certain sense of frustration with trying to motivate people to learn about the stress-energy tensor. It's something they really need to know, but the resistance I see to learning about it is not just limited to the thread. It could be my approach, but I've tried several and they generally don't seem to work (it's hard to tell over the internet, but that's my overall impression). Even when, as in this thread, we see people running into issues that they know are there, and are looking for answers. They don't seem to want to go down this route to get the answers, though :(.

Some of the pedagogical issues with the stress-energy tensor are that the developmental papers are mostly not written in English (and are hard to come by). Textbooks do introduce the topic, but at an abstract level but don't really motivate it that well in my opinion.

My own attempts to motivate the stress-energy tensor have met with somewhat limited success to date. So I don't feel I've done any better than the textbooks, which for the most part introduce the topic but don't really attempt to motivate it.

 

[liuxinhua]

Thank you very much, Pallen. We should think that the potential energy of born rigid body body is not a relativistic scalar.
My questions have been solved.

However, I insist on my view that the potential energy of born rigid body is a relativistic scalar. Or the rest energy of born rigid body is a relativistic scalar.

We can strictly deduce that the rest energy of a born rigid body is not a relativistic scalar. Since it is derived, there is a premise or basis. Some of these is that the default special relativity is correct, the conservation of momentum is correct, and what Pervect says is that the $K$ we use is flat, and so on. This is one aspect of the problem.

Why do I insist that the rest energy of born rigid body is a relativistic scalar?I think it in another way.
It is an inborn rigid body. I think this is one of its characteristics.
If the rest energy of a born rigid body changes, then it is no longer a born rigid body. Maybe what I call born rigid is different from the expression of the born rigid body in your mind

Unless my model is not a born rigid body.

(In fact, the rest energy of a born rigid body consists of two parts: the potential energy of a born rigid body, and the actual particles or the material in the form of physical existence. So we can replace the statement "the potential energy of a born rigid body does not change" with "the rest energy of a born rigid body does not change.")

 

[liuxinhua]

I suspect you haven't looked at the formal definition of Born rigidity.

Maybe what I call born rigid is different from the expression of the born rigid body in your mind

I have not seen the formal definition of natural Born rigidity, but I think we mean the same thing, Though I'm not sure it.

For any object measured in an inertial frame: $the\ sum \ rest \ masses=\frac {the \ rest \ energy } {c^2}$

 

[PeterDonis]

I have not seen the formal definition of natural Born rigidity

The formal definition of Born rigid motion of an object is that the congruence of worldlines describing the object has zero expansion and zero shear. Since this is an "A" level thread, you should know what those terms mean mathematically.

 

[PAllen]

I have not seen the formal definition of natural Born rigidity, but I think we mean the same thing, Though I'm not sure it.

For any object measured in an inertial frame: $the\ sum \ rest \ masses=\frac {the \ rest \ energy } {c^2}$

This is trivially false. The sum of rest masses for spinning disk does not include kinetic energy contributions to the rest energy.

 

[liuxinhua]

This is trivially false. The sum of rest masses for spinning disk does not include kinetic energy contributions to the rest energy.

The rest energy I understand does not include kinetic energy.

In an inertial reference frame such as $K$, an object is observed.

The total energy （$E$）contains energy includes its rest energy and the kinetic energy relative to $K$;

The invariant mass corresponds to the energy $\sqrt {(E^2-\left\|{p}^2\right\|c^2)}$, it contains its rest energy and the kinetic energy relative to MCIF, (the kinetic energy relative to MCIF is not the kinetic energy relative to $K$ ). Maybe physicists call this energy as rest energy. But I think the rest energy of a system should be the following energy.

Rest energy is the amount that add up to all the energy of the system measured from the respective MCIF of each part (infinitely small in length width and height) for each part of the system. The rest energy of a system does not contain any kinetic energy (relative to $K$ or relative to MCIF), corresponding to the sum of the rest masses of the system.


For two particles (their rest mass is $m_0$ each, they do not constitute a Born rigid system) moves at velocity $u_1$ and $u_2$ along $x$ direction.

Their total energy is $E=m_0γ(u_1)c^2 + m_0γ(u_2)c^2$.

Their rest energy is $m_0 c^2 + m_0 c^2$.

And $\sqrt {(E^2-\left\|{p}^2\right\|c^2)}$=$\sqrt {{(m_0γ(u_1)c^2 + m_0γ(u_2)c^2)}^2- {(m_0γ(u_1) u_1+ m_0γ(u_2) u_2) }^2 c^2}$

$E$>$\sqrt {(E^2-\left\|{p}^2\right\|c^2)}$> $m_0 c^2 + m_0 c^2$

The total energy of a Born rigid body may be changed. The energy $\sqrt {(E^2-\left\|{p}^2\right\|c^2)}$ of a Born rigid body may be changed. The rest energy of a Born rigid body is a constant.

For an arbitrary system, its rest energy is not necessarily conserved. Even for isolated systems, the rest energy is not necessarily conserved.

 

[liuxinhua]

Here is one point.
The sum of the rest masses at each location is not the system's invariant mass.
But the sum of the rest energy at each location is the rest energy of the system.