Discussion Overview
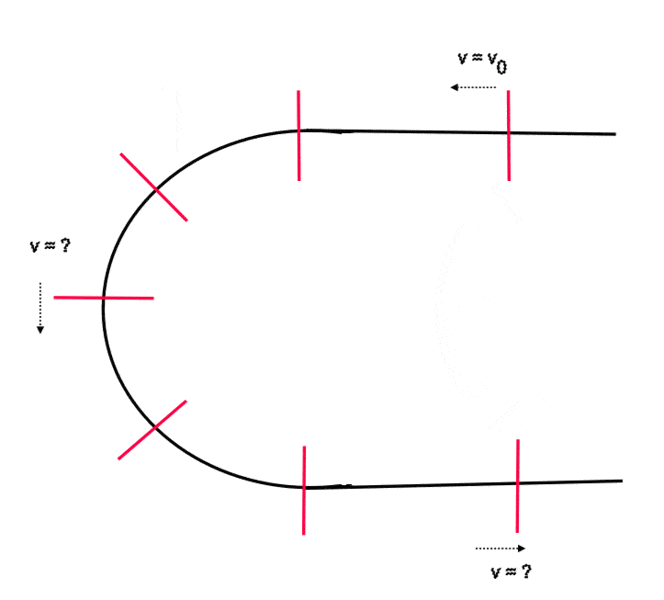
The discussion revolves around a classical mechanics problem involving the motion of a mass constrained to a rail, specifically a thin rigid rod moving frictionlessly along a rail that transitions from a straight path to a curved section. Participants explore the implications of this setup on the speed of the rod at various points, particularly at the apex of the curve and upon returning to the straight section, while considering the forces and energy involved in the motion.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants assert that if the system is frictionless and the rail is immobile, the velocity of the rod's center remains constant throughout its motion.
- Others argue that a central reaction force from the rail must act on the rod, suggesting that there are external forces involved despite the frictionless condition.
- There are claims that during the curved motion, both translational and rotational kinetic energy must be considered, leading to a lower velocity at the apex of the curve, which then returns to the initial value upon exiting the curve.
- Some participants question the necessity of instantaneous changes in speed as the rod transitions between straight and curved sections, suggesting that a more gradual curvature would avoid the need for infinite forces.
- There is a contention regarding the application of kinetic energy formulas, with some asserting that both translational and rotational kinetic energies can be applied simultaneously, while others disagree.
- Participants discuss the implications of impact forces at the transitions between straight and curved sections, with some suggesting that these forces must be infinite to account for the instantaneous changes in motion.
- Concerns are raised about how angular velocity can change without friction, with some proposing that normal contact forces at multiple points of contact during the transition could account for this change.
Areas of Agreement / Disagreement
Participants express multiple competing views regarding the forces acting on the rod, the application of energy conservation principles, and the nature of the transitions between motion states. The discussion remains unresolved, with no consensus reached on the validity of the various claims and interpretations presented.
Contextual Notes
Participants highlight the need for a physically realistic model, suggesting that assumptions about infinite forces or mass may not be necessary if the problem is framed differently. The discussion also points to limitations in the assumptions made about the nature of the forces and the motion of the rod.