Falling apple inside a space centrifuge

[artriant]

When a mass is in a circular motion and suddenly gets released by its centripetal force, it will continue traveling in a straight path (tangent to the circle and perpendicular to the radius in the moment of release) if no other forces acting.

So let’s make a case: We have a space centrifuge r=250m that provides "an artificial gravity or an accelaration equal to moons gravity, the entire structure is cruising freely in free fall let's say in GEO orbit. The linear speed at the circumference (which is also happening to be the ground inside the space station), is Uc =20.13715 m/s. Our test subject is going to be an apple that is fixed inside the rotating frame and “hovering” 10 m above the “ground”, the point exactly below the apple we will nickname it “ground zero”, and we will also assume that we don’t have any air or obstacles or other external forces. Now when we let the apple to “fall” observers inside in the outer region of the space station - near it, will witness that it follows a curved path which is affected by the Coriolis Fictious Force. Problem is that i can't use physics, so i used geometry to predict the offset.

We draw the station (a big circle)in the blackboard and a straight line perpendicular to the position of the apple in the moment of release. We found the impact point but did we just solved the problem? Nop, the linear speed of the apple is different than the linear speed of the outer region mainly because we have 10m difference in radius. To find the U of the apple (Ua) we can use the linear speed at the circumference Uc and because it is proportional to r we can find for any raidus with the rule of three:

Ua (m/s) / 240(m) = Uc (m/s) / 250(m),,, so Ua (m/s)=240(m)*Uc (m/s)/250(m) => Ua=19,331664(m/s)

Right after the release, the apple will travel freely 70(m) in a straight line AB of a triangle ABC that has the C connected to the center of the station (center of rotation), with angles ∠ACB=16.26° ∠ CBA=73,74° ∟BAC=90°

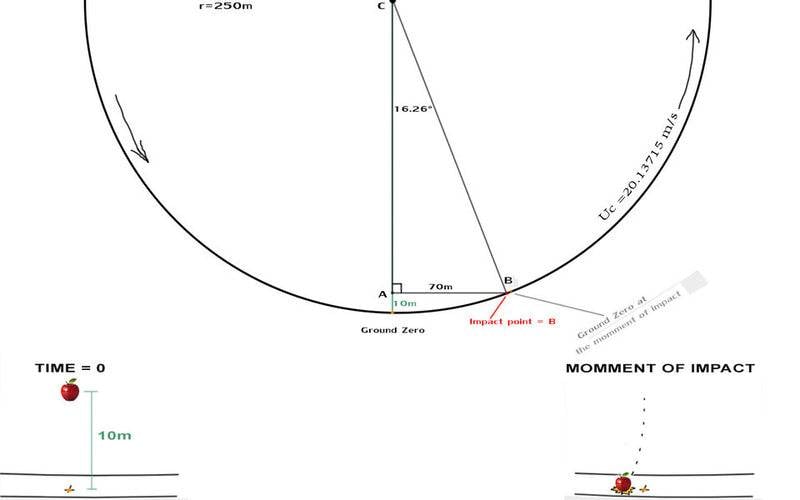
Since we know the speed of the apple we can find the amount of time (t1) till it travels from point A to point B, rule of three: t1(sec)/70m 1sec/20.13715m => t1sec=70*1/20.13715 = t1=3,621 (sec)

So regardless of path in our experiment we already know that the apple is going to “fall” for 3,621 (sec) till it colides with the ground.

In the same amount of time, the host is going to rotate 16.26°

That angle coresponds to a length of arc X1(m) = 3,621(sec)*20.13715(m)/1(sec) => X1= 72,9166~ (m)

The length of the arc (in the circumference) from ground zero to the hit point 'B' is :
X2/quarter of circle (meters)= 16,26/90 (degrees) =>X2=(392,7*16,26)/90 => X2=70,9478m

If we subtract X2-X1 we get the offset measured in a length of arc = 1.968866~ m (absolute value)

So a camera focused on the ground zero, will record an apple that is missing the “target” (ground zero)by a whole 1,96 m, the measuring tool should be placed touching the ground parallel to circumference and against the direction of spinning, the apple kind of left behind while falling, like it couldn’t catch up the faster moving ground of the space station. Others explain that behavior of the falling apple inside a space centrifuge "like it is blown by a wind that flows against the direction of spinning".
----
My question is how do i solve the same problem with physics, i can predict the ofset here which is handy, but can't predict the exact path, or where the apple is going to be at any point in time, in a rotating reference frame. I really want to visualize that for varius setups. I think this will be very baisic in the future. Thanks for any replies.

 

[Work Hard Play Hard]

What's the speed of the station where the apple is dropped?

 

[artriant]

The space station is spinning with a linear tangetial speed Uc =20.13715 m/s at the circumference which is enough to produce Artifial Gravity 0.1654g (moon) for that radius 250m. Maybe i had to use the symbol V instead i just capitalized the lowercase symbol looks like a u sorry for that.

 

[Work Hard Play Hard]

Sorry my fault. How does this induced gravity as you call it differ from actual gravity? What is it if not gravity?

 

[mfb]

You used physics to solve the problem: Newtonian motion in an inertial system.

You can consider the problem in the rotating reference frame, then you have to solve a differential equation with centrifugal force and coriolis force. The calculation becomes much more complicated, but the result will be the same.

 

[A.T.]

How does this induced gravity as you call it differ from actual gravity?

Look at the picture. The apple doesn't hit the point it is released above (the point it's gravity points to at release).

 

[A.T.]

predict the exact path, or where the apple is going to be at any point in time, in a rotating reference frame.

Two equivalent ways to do this:
- Use the inertial frame as you already did, to predict the position of the apple and orientation of the station for any time point, then transform the apple position into the rotating frame of reference.
- Use the rotating frame of reference as mfb suggested, which involves inertial forces acting on the apple.

 

[artriant]

Sorry my fault. How does this induced gravity as you call it differ from actual gravity? What is it if not gravity?

Im not really sure for the terms that ill use, but I think you can surelly call this Artificial Gravity and you can add maybe if you want "generated via spinning" to define what type of artificial, or you can use "with centrifugation in space". We talking about a substitute of gravity not real gravity, that's why we need to take into calculation circular motion laws to predict even the simple case of a falling apple. In chemistry they use the term efective gravitational force to describe the outwards effect, but since gravity is accelaration, one can use the term centrifugal accelaration *(in rotating reference frame). But i bet in a future space station the residents in everyday lives they will just use the term gravity cause it becomes pretty similar on big radiuses and close to 1g.

Main differences the Artificial Gravity here is proportional to radius so even if we just go up 1 meter we will weight less and the oposite. Falling things follow curved paths, launced things follow unusual curved paths as well, plus if we walk towards the direction of spin we will gain weight and the opossite. But all these effects become less imporant in big radiuses if our target is a "gravity" simmilar to Earth.

Thanks mfb, hehe yep i used physics afterall, but preety basic, i panic when i hear vectors and such.
Ill post an attempt when i get my head around it, I found an interestng paper.

And thnx A.T, you are right actually, i didnt realized i already have the position of the apple at any given time.
Ofourse ill need to find a way to quickly translate that in inertial reference frame, maybe more trigonometry, by the way we have same initials

 

[Andy SV]

Geometry is physics like star gazing is astronomy ... The naked hart of it

 

[A.T.]

i panic when i hear vectors and such ... maybe more trigonometry,

Using vectors and a rotation matrix is a simple way to avoid repetitive trigonometry derivations.

 

[artriant]

Just a note, it looks like an offset simmilar to the example, is a constant for a specific size of space centrifuge (radius), so regardless of artificial gravity amount ( regardless how fast we spin different ω and V), we get same offset for specific r and h. Unless of course the structure is not spinning at all hence we have zero g and apple doesn`t fall at all. I spend a few hours y/day was trying to fix calculations that was not broken

So here is a table with offsets for apples "that fall from 2m height" in space centrifuges of varius size.

Radius of the host | Offset
5(m) | 2.73(m)
50(m) | 0.39(m)
500(m) | 0.12~(m)
1800(m) | 6.2(cm)
5(km) | 3.7(cm)
50(km) | 1.2~(cm)
100(Km) | 8.4(mm)
10K (Κm) | 8(μ)
100K (Km) | 3~(μ)
1M (Km) | 1~(μ)

 

[Work Hard Play Hard]

Look at the picture. The apple doesn't hit the point it is released above (the point it's gravity points to at release).

Im not really sure for the terms that ill use, but I think you can surelly call this Artificial Gravity and you can add maybe if you want "generated via spinning" to define what type of artificial, or you can use "with centrifugation in space".

Thanks for the replies but they were rhetorical questions. Poorly done I gather?

In the 60's NASA gave it a name, Rotogravic Environment. Something I learned in a lecture along with this, In the early years NASA was protective of it's work being defined by popular culture rather then themselves so they kept a lot to themselves. The term Rotogravic Environment came from an MD because he thought too often solutions to problems weren't taking into account the solutions were for people. Solutions that don't allow for people aren't solutions.