Austin0 said:
From these posts I seem to understand that my initial grasp was basically correct as far as the behavior if not on any implications of mass.
Austin0 said:
it is not a totally absurd topic of speculation.
JesseM said:
It is absurd if you are both postulating that photons move at c and that they have mass. Any paper speculating about photon mass is presumably speculating that photons actually move slower than c (where c is defined to be the fundamental constant that appears in the Lorentz transformation/time dilation equation/etc., not defined as the speed of photons).
As per early post above I was not postulating anything , just musing in print.
I quickly let it go completely as it wasn't really the point.
On the other hand having been pressed it is not really without some justification.
It seems to me that whether photons move exactly at the upper possible limit or not is not important. The derived value c for photons as it stands, appears to be correct for all EM interactions which also appears fundamental to everything else too.
Austin0 said:
I mean that a photon emitted transversely in a moving system and reflected within that system bounces straight up and down just like a Newtonian ball. It retains the forward motion of the system. i.e. conserved forward momentum. It is not independent of the motion of the source except with regard to emissions along the path of motion.
Austin0 said:
That with emissions in the direction of motion the sH component is not conserved at all i.e. does not contribute to the velocity vector c
JesseM said:
What do you mean "does not contribute to the velocity vector c"? Do you disagree that in this case s_H^2 + s_V^2 = c^2? That looks like a "contribution" to the total speed of c to me. For example, we might have sH=0.8c and sV=0.6c, so then it'd be true that (0.8c)^2 + (0.6c)^2 = (0.64 + 0.36)*c^2 = c^2.
Emmissions along motion path are c regardless of the velocity of the emitter no?
SO the x or H component of the source does not contribute.
Wrt a photon emitted directly to the rear or at an acute angle to the rear what contribution to the resulting velocity vector does the forward x component of the emitter make??
Austin0 said:
Don't you find it somewhat [read extremely] curious that photons are not totally independent of the motion of the source and do act like massive particles wrt transverse emissions?
JesseM said:
No. If the photon direction was independent of the source, that would falsify relativity, since there would be a single preferred frame where a photon emitted by a tube pointing in one direction would actually travel in the same direction. The first postulate of relativity says that the laws of physics should work the same way in all inertial frames, which means that if experimenters in inertial windowless ships moving at different velocities all perform the same experiment, they should all get the same result--the first postulate would be violated if an experimenter in one frame found that light exited the emitter parallel to the orientation of the emitter, but an experimenter in a different frame found that it exited at an angle relative to the orientation of the emitter.
Are you familiar with the http://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/Special_relativity_basics/index.html#Light1 thought-experiment? This thought-experiment actually depends on the fact that light always travels parallel to the emitter in the emitter's rest frame in order to derive the time dilation equation.
Austin0 said:
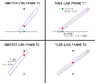
Hi Bob S ...I am afraid I was not clear enough in my post.
The tube and detector are both at rest in the lab frame. There is clearly no problem if the tube is in the emitter frame otherwise a light clock could not work.
You are looking at things from the perspective of consistency with SR , I wasnt questioning this but simply looking at the physics and finding it strange that a massless wave would act like a massive particle.
Austin0 said:
With regard to a massive particle say a bullet that is rotating around the axis of motion: in a relative frame the forward momentum would result in a sideways drift relative to the spin??
JesseM said:
I don't know what you mean by "sideways drift relative to the spin". The linear momentum of the center of mass is conserved as long as no forces are acting, so in zero gravity a spinning bullet will travel in a straight line just like a nonspinning bullet.
I meant that in the lab frame the bullet spin would remain parallel to the y-axis so the conserved x motion would be sideways relative to the spin.
Or conversely it would be tilted relative to the linear path it was traveling in the lab.
Austin0 said:
Wrt a photon this is not such a comfortable picture. If we consider a photon as a traveling waveform this would mean it would be out of phase along an orthogonal front relative to its linear motion, yes?
It would seem to be more realistic to view the angle derived from the vector sum of conserved momentum as an actual propagation angle with the wave front in phase, relative to travel,
JesseM said:
Don't understand this sentence. "Out of phase" with what other wave, exactly?
Out of phase with itself , tilted relative to the path of motion .
Since that post I have followed a link Bob S posted to another thread and another link where on the last page (13 ), last paragraph of a paper I found the following which is related to Terrell rotation but also seems to answer my question here
""""One can do these same calculations from any selected observation angle and
nds similar results. The image (eye or photographic) appears to be a cube rotated
by the aberration angle.
The key issue is that one is observing with light emitted from the object (cube
in our example).
In relativity light propagates with constant speed c independent of
the observer's or source speed and the key point here is that the wave front always
remains perpendicular to the direction of propagation. The only thing that changes
is the direction of propagation (and thus wavefront angle) which is what we call
relativistic aberration. Thus an image in one frame remains an image in the other
and only the angle of observation changes.
This statement is true for the case of a small object which subtends a small
solid angle. As one goes to larger angles, the aberration changes and a larger solid
angle object would be rotated and distorted by the variation in aberration angle
across the object being viewed.