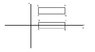
Calculating Ixy | Plane ABCD, PQRS Symmetry & Moment of Area

  • Thread starter Thread starter phydis
  • Start date Start date
AI Thread Summary
For a plane figure symmetrical along the X-axis, the product of moment of area Ixy is zero when calculated through the centroid. This occurs because each area element on one side of the axis has a corresponding element on the opposite side, resulting in equal and opposite contributions to the integral. To compute Ixy for a rectangle like PQRS, the parallel axis theorem can be utilized. This theorem allows for the calculation of moments of area by shifting the axis to the centroid. Understanding these principles is crucial for accurate moment of area calculations in structural analysis.
phydis
Messages
28
Reaction score
0
Here as shown in the diagram,

(1)Is Ixy zero for plane ABCD symmetrical along X axis? If yes, how it happens?
(2)How can we calculate Ixy for the plane PQRS ?

Ixy = the product of moment of area.

Thanks!
 

Attachments

  • Ixy.jpg
    Ixy.jpg
    7.7 KB · Views: 2,534
Physics news on Phys.org
For any plane figure with an axis of symmetry, Ixy = 0 for coordinate axes thru the centroid of the figure.

To confirm this, examine the definition of Ixy = Int(x*y)dA For every element of area dA which lies on one side of the axis of symmetry, there will be a corresponding element of area lying on the opposite side which is the same distance from the axis. When you add up all of these elements of area multiplied by x*y, the integral is necessarily equal to zero.

To calculate the Ixy of rectangle PQRS, apply the parallel axis theorem.
 
  • Like
Likes 1 person
Thread 'Gauss' law seems to imply instantaneous electric field propagation'

Thread 'Gauss' law seems to imply instantaneous electric field propagation'

Imagine a charged sphere at the origin connected through an open switch to a vertical grounded wire. We wish to find an expression for the horizontal component of the electric field at a distance ##\mathbf{r}## from the sphere as it discharges. By using the Lorenz gauge condition: $$\nabla \cdot \mathbf{A} + \frac{1}{c^2}\frac{\partial \phi}{\partial t}=0\tag{1}$$ we find the following retarded solutions to the Maxwell equations If we assume that...
View full post »

Thread 'Do electron density waves accompany EM waves in coaxial cables?'

Maxwell’s equations imply the following wave equation for the electric field $$\nabla^2\mathbf{E}-\frac{1}{c^2}\frac{\partial^2\mathbf{E}}{\partial t^2} = \frac{1}{\varepsilon_0}\nabla\rho+\mu_0\frac{\partial\mathbf J}{\partial t}.\tag{1}$$ I wonder if eqn.##(1)## can be split into the following transverse part $$\nabla^2\mathbf{E}_T-\frac{1}{c^2}\frac{\partial^2\mathbf{E}_T}{\partial t^2} = \mu_0\frac{\partial\mathbf{J}_T}{\partial t}\tag{2}$$ and longitudinal part...
View full post »
Thread 'Recovering Hamilton's Equations from Poisson brackets'

Thread 'Recovering Hamilton's Equations from Poisson brackets'

The issue : Let me start by copying and pasting the relevant passage from the text, thanks to modern day methods of computing. The trouble is, in equation (4.79), it completely ignores the partial derivative of ##q_i## with respect to time, i.e. it puts ##\partial q_i/\partial t=0##. But ##q_i## is a dynamical variable of ##t##, or ##q_i(t)##. In the derivation of Hamilton's equations from the Hamiltonian, viz. ##H = p_i \dot q_i-L##, nowhere did we assume that ##\partial q_i/\partial...
View full post »

Similar threads

Is Moment of Inertia Dependent on Surface Movement Away from Axis?
Replies
9
Views
2K
A Electric and magnetic field lines in a plane wave of finite extent
Replies
1
Views
1K
1st, 2nd and mass moment of inertia
Replies
6
Views
5K
ABCD matrix formalism for concave mirror
Replies
5
Views
3K
How Do You Calculate the Moment of Inertia for Combined Square Laminas?
Replies
3
Views
3K
Product Second Moment of Area Ixy - Help
Replies
1
Views
20K
Calculating Second Moment of Area: How-To & Examples
Replies
12
Views
5K
How does metal sphere determine the potential of the plane by symmetry?
Replies
15
Views
2K
B Beam on an inclined plane
Replies
4
Views
179
B Will there always be a vector product for 2 vectors in a 3d plane?
Replies
8
Views
2K

Hot Threads

Recent Insights

Back
Top