2 blocks connected by a metal pull on an inclined plane

[hannibalisfun]

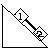
The problem is I have two blocks on an inclined plane. They are connected by a metal rod. The bottom(2) mass provides the dominate force. Fiction is involved. They have different kinetic coefficients of friction. I need to know the acceleration of the system and the tension in the rod. Picture in diagram 1.

If you could provide help on one other problem that would help a lot.

A plane is turning. Yoy know the angle its wings are tilted and its speed. How do you find the radius of the turn? Assume all force come from aerodynamic lift.

 

[hannibalisfun]

Sorry I didn't know you wanted me show my efforts at the problem. well for the first one most of my work has been finding out what the value of the forces acting on the block are like the frictional force or the force of gravity parallel to the plane for both blocks. Unfortunately I don’t have my work with me or the even the problem it self. For the acceleration I was thinking I could just add the forces of gravity parallel and subtract the 2 frictional force then divided by total mass but I wasn’t sure how tension factors into that. As for the tension in the rod I have no clue as of yet because I have started that part but even a little hint on that part would greatly be appreciated.
As for the plane problem I tried to use the formula for centripetal force, g * cos(angle) for the force, but I keep getting the wrong answer. Also on this problem I I were given a time instead of speed is the problem still solvable.

 

[OlderDan]

Sorry I didn't know you wanted me show my efforts at the problem. well for the first one most of my work has been finding out what the value of the forces acting on the block are like the frictional force or the force of gravity parallel to the plane for both blocks. Unfortunately I don’t have my work with me or the even the problem it self. For the acceleration I was thinking I could just add the forces of gravity parallel and subtract the 2 frictional force then divided by total mass but I wasn’t sure how tension factors into that. As for the tension in the rod I have no clue as of yet because I have started that part but even a little hint on that part would greatly be appreciated.
As for the plane problem I tried to use the formula for centripetal force, g * cos(angle) for the force, but I keep getting the wrong answer. Also on this problem I I were given a time instead of speed is the problem still solvable.

You can treat the two blocks connected by the rod as one object to find the acceleration as you said. Make sure you account for all of the external forces (gravity components and friction) Once you know the acceleration, you can find the tension in the rod by focusing on one of the blocks and accounting for all of the forces acting to give it the acceleration you already calculated.

For the plane the lift does two things. It supports the weight of the plane and it provides the centripetal force required to move the plane in a horizontal circular path