Johnls
- 11
- 0
I'm talking here about this situation:
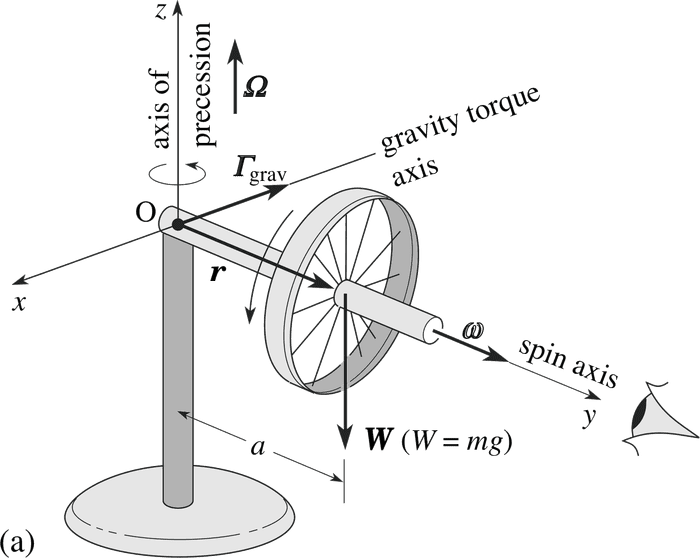
The explanation which is usually given as to why there is a precession, is that the torque is perpendicular to the angular momentum and the angular momentum changes in the direction of the torque.
A few things I don't understand about it:
1. The torque is relative to point O but the angular momentum is relative to the center of the wheel. When you derive that torque is the change in the angular momentum, don't you assume that they are both calculated relative to the same point?
2. Why doesn't it work for low angular momentums?
The explanation which is usually given as to why there is a precession, is that the torque is perpendicular to the angular momentum and the angular momentum changes in the direction of the torque.
A few things I don't understand about it:
1. The torque is relative to point O but the angular momentum is relative to the center of the wheel. When you derive that torque is the change in the angular momentum, don't you assume that they are both calculated relative to the same point?
2. Why doesn't it work for low angular momentums?