2D Fourier transform orientation angle

[roam]

The orientation of frequency components in the 2-D Fourier spectrum of an image reflect the orientation of the features they represent in the original image.

In techniques such as nonlinear microscopy, they use this idea to determine the preferred (i.e. average) orientation of certain features in a given image (e.g. the orientation of collagen fibers). For example here for different regions of interest, they obtained the power spectra (shown below in binary), and using that they inferred the orientation angle.

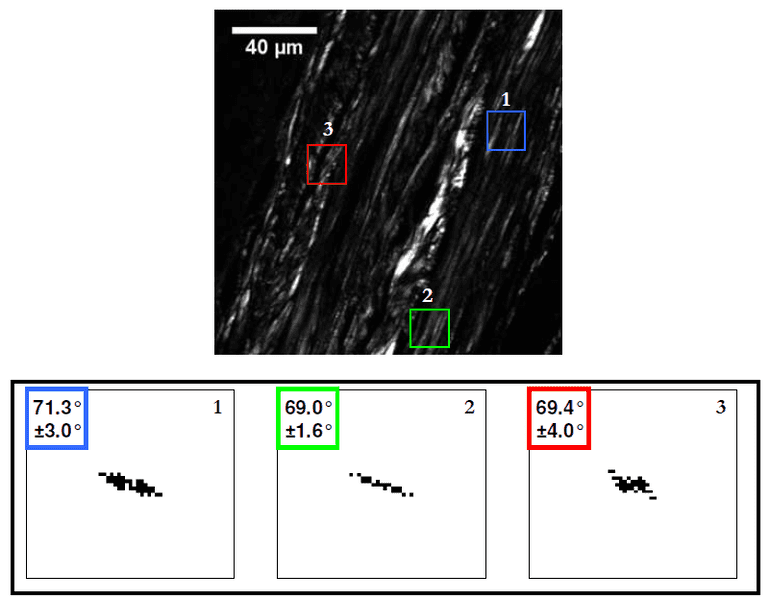
So, I am not sure how they would measure the angle of the FT. Are there equations for finding the tilt angle of a certain frequency component?

I believe when they find all the angles, they would do a fitting to get the average orientation. The $\pm$ in the picture above is the standard deviation – the number of fibers that deviate from the preferred orientation.

How would an algorithm for finding the angle look like? Unfortunately, the papers did not explain this in any detail.

Any explanation would be greatly appreciated.

 

[marcusl]

Actually it’s at right angles. The FT of a narrow feature is broad in the direction normal to it, etc.

 

[roam]

So, for example, if you have a single sinusoid with a spectrum like this:

The FT has the same orientation (or is at right angles) with the direction of the feature. How would you calculate the angle that the FT is making with respect to the x/y axis?

Is there an equation or an algorithm that you can use?

 

[marcusl]

Take the arctangent of the absolute value of the ratio of the Y coefficient over the x coefficient of the FFT.