akorn3000
- 7
- 0
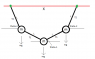
Suppose you have 3 balls, all of equal mass, M. They are connected to each other by equal-length (each length L) strings of negligible mass, such that one ball is suspended in the middle and the two balls at the end are themselves suspended from the ceiling at two points, a distance X from one another. Using M, X, and L, how would I go about finding the exact angles the balls make with the horizontal? I tried summing the forces and the moments, but I think I must be doing something wrong. Any help would be appreciated.