3 objects connected by ropes (tension)

[metalmagik]

The drawing shows three objects, with m1 = 11.5 kg and m2 = 23.5. They are connected by strings that pass over massless and frictionless pulleys. The objects move, and the coefficient of kinetic friction between the middle object and the surface of the table is 0.100.

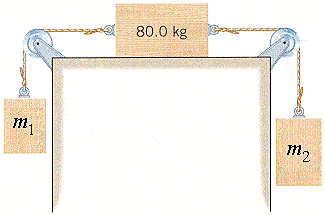
(a) What is the acceleration of the three objects?

(b) Find the tension in each of the two strings.

I made FBDs for these three blocks...and what I got ended up being the acceleration for the middle block, which came out to be 1.7 m/s^2. How do I find the acceleration of ALL three objects?? Any help is greatly appreciated, this is for a webassign and I would really like to get this correct.

 

[Hootenanny]

I made FBDs for these three blocks...and what I got ended up being the acceleration for the middle block, which came out to be 1.7 m/s^2. How do I find the acceleration of ALL three objects?? Any help is greatly appreciated, this is for a webassign and I would really like to get this correct.

HINT: All three block accelerate at the same rate.

 

[metalmagik]

so if I find the mass of ONE block, I've found the mass at which all three blocks accelerate? or must I add them up?

 

[metalmagik]

I do not understand how to achieve the acceleration when you don't have the tension forces. You need those to achieve Fnet do you not?

 

[radou]

I do not understand how to achieve the acceleration when you don't have the tension forces. You need those to achieve Fnet do you not?

All you have to do is slow down. Take the mass m2 and draw a FBD for it. As Hootenanny said, all masses accelerate at the same rate. Apply Newton's second law to mass m2. Then do the same thing for the mass in the middle. And then for the left one. Look at the equations you got and try to solve for a.

 

[metalmagik]

Fnet = ma...so...for the right one what is the Fnet? I still don't understand how one does this without the Force of tension. I'm very confused.

 

[radou]

Fnet = ma...so...for the right one what is the Fnet? I still don't understand how one does this without the Force of tension. I'm very confused.

OK, let's take the right mass, m2. The forces acting on it are the gravitational force G = m2*g and the tension in the right rope, let's call it T2. So, tkat makes Fnet = T2 - G = T2 - m2*g. When you use Newton's second law, you have Fnet = m2*a, i.e. T2 - m2*g = m2*a. Now do the same thing for the other masses.

 

[metalmagik]

Ok so for the center one I have T1-F+T2 = Mc*a

and for the left one I have T1 - m1g=m1a

is this correct?

 

[radou]

Ok so for the center one I have T1-F+T2 = Mc*a

and for the left one I have T1 - m1g=m1a

is this correct?

Correct, but you made a mistake for the central mass. T1 and T2 are pointing in opposite directions. So, it should be -T1 - F + T2 = Mc*a.

 

[metalmagik]

oh I see. How can I now calculate acceleration from this?

 

[radou]

oh I see. How can I now calculate acceleration from this?

You have three equations now, right? Well, use the equations for the right and left mass, and express them in a form T2 = ... and T1 = ... Then plug T1 and T2 into the equation for the central mass and you'll be able to calculate the acceleration a out of this equation directly.

 

[metalmagik]

I have -(m1g+m1a)-Ff+(m2g+m2a) = ma

Is it possible for me to set the accelerations equal to 1 making them insignificant in the equation?

 

[radou]

I have -(m1g+m1a)-Ff+(m2g+m2a) = ma

Is it possible for me to set the accelerations equal to 1 making them insignificant in the equation?

I don't understand what you're trying to ask. You now know everything in the equation, just solve for a.

 

[metalmagik]

Oh I see, I got .871 m/s^2

Is this correct? I am going CRAZY with all of this haha

 

[radou]

Oh I see, I got .871 m/s^2

Is this correct? I am going CRAZY with all of this haha

If you followed the equation, and if you didn't do any 'calculator typos', it should be correct.

 

[metalmagik]

wow okay I got it wrong...I guess it must've been my fault.