- #1
mathmari
Gold Member
MHB
- 5,049
- 7
Hey! 
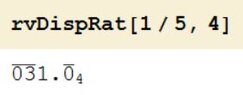
I want to find the $4$-adic expansion of $\frac{1}{5}$. I have done the following: $\displaystyle{\frac{1}{5}\equiv a_0\pmod 4 \Rightarrow a_0\equiv \frac{1}{5}\pmod 4}$
We multiply by $5$ and we get $\displaystyle{5a_0\equiv 1\pmod 4}$.
The only residue of division by $4$ that solves this is $a_0=1$. Then we have $\displaystyle{\frac{1}{5}-1\equiv 4a_1 \pmod {4^2} \Rightarrow -\frac{4}{5}\equiv 4a_1\pmod {4^2}}$.
We divide by $4$ and we get $\displaystyle{-\frac{1}{5}\equiv a_1\pmod {4}}$.
We multiply then by $5$ and we get $\displaystyle{-1\equiv 5a_1\pmod {4}\Rightarrow 5a_1\equiv -1 \pmod 4 \Rightarrow 5a_1\equiv 3\pmod 4 \Rightarrow a_1\equiv 3\pmod 4}$. The only residue of division by $4$ that solves this is $a_1=3$. Then we have $\displaystyle{\frac{1}{5}-1-3\cdot 4\equiv 4^2a_2 \pmod {4^3} \Rightarrow -\frac{4}{5}-3\cdot 4\equiv 4^2a_2\pmod {4^3}}$.
We multiply by $4$ and we get $\displaystyle{-\frac{1}{5}-3\equiv 4a_2\pmod {4^2}\Rightarrow -\frac{16}{5}\equiv 4a_2 \pmod {4^2}}$, we multiply then by $5$ and we get $\displaystyle{-16\equiv 20a_2\pmod {4^2} \Rightarrow 0\equiv 4a_2 \pmod {4^2} \Rightarrow 4a_2\equiv 0\pmod {4^2}}$. We divide by $4$ and we get $\displaystyle{a_2\equiv 0\pmod {4}}$. The only residue of division by $4$ that solves this is $a_2=0$. Then we have $\displaystyle{\frac{1}{5}-1-3\cdot 4\equiv 4^3a_3 \pmod {4^4} \Rightarrow -\frac{4}{5}-3\cdot 4\equiv 4^3a_3\pmod {4^4}}$.
We divide by $4$ and we get $\displaystyle{-\frac{1}{5}-3\equiv 4^2a_3\pmod {4^3}\Rightarrow -\frac{16}{5}\equiv 4^2a_3 \pmod {4^3}}$, then we divide by $4^2$ and we get $\displaystyle{ -\frac{1}{5}\equiv a_3 \pmod 4}$. Then we multiply by $5$ and we get $\displaystyle{ -1\equiv 5a_3 \pmod 4\Rightarrow 5a_3\equiv -1 \pmod 4 \Rightarrow a_3\equiv 3 \pmod 4 }$. The only residue of division by $4$ that solves this is $a_3=1$.
Then we have $\displaystyle{\frac{1}{5}-1-3\cdot 4-4^3\equiv 4^4a_4 \pmod {4^5} \Rightarrow -\frac{4}{5}-3\cdot 4-4^3\equiv 4^4a_4\pmod {4^5}}$.
We divide by $4$ and get $\displaystyle{-\frac{1}{5}-3-4^2\equiv 4^3a_4\pmod {4^4}\Rightarrow -\frac{16}{5}-4^2\equiv 4^3a_4 \pmod {4^4}}$, then we divide by $4^2$ and get $\displaystyle{ -\frac{1}{5}-1\equiv 4a_4 \pmod 4^2 \Rightarrow -\frac{6}{5}\equiv 4a_4 \pmod {4^2}}$. We multiply then by $5$ and get $\displaystyle{ -6\equiv 20a_4 \pmod {4^2}\Rightarrow 20a_4\equiv -6 \pmod {4^2} \Rightarrow 4a_4\equiv 10 \pmod {4^2} }$.
This doesn't have a solution, right?
Where have I done something wrong? (Wondering)
I want to find the $4$-adic expansion of $\frac{1}{5}$. I have done the following: $\displaystyle{\frac{1}{5}\equiv a_0\pmod 4 \Rightarrow a_0\equiv \frac{1}{5}\pmod 4}$
We multiply by $5$ and we get $\displaystyle{5a_0\equiv 1\pmod 4}$.
The only residue of division by $4$ that solves this is $a_0=1$. Then we have $\displaystyle{\frac{1}{5}-1\equiv 4a_1 \pmod {4^2} \Rightarrow -\frac{4}{5}\equiv 4a_1\pmod {4^2}}$.
We divide by $4$ and we get $\displaystyle{-\frac{1}{5}\equiv a_1\pmod {4}}$.
We multiply then by $5$ and we get $\displaystyle{-1\equiv 5a_1\pmod {4}\Rightarrow 5a_1\equiv -1 \pmod 4 \Rightarrow 5a_1\equiv 3\pmod 4 \Rightarrow a_1\equiv 3\pmod 4}$. The only residue of division by $4$ that solves this is $a_1=3$. Then we have $\displaystyle{\frac{1}{5}-1-3\cdot 4\equiv 4^2a_2 \pmod {4^3} \Rightarrow -\frac{4}{5}-3\cdot 4\equiv 4^2a_2\pmod {4^3}}$.
We multiply by $4$ and we get $\displaystyle{-\frac{1}{5}-3\equiv 4a_2\pmod {4^2}\Rightarrow -\frac{16}{5}\equiv 4a_2 \pmod {4^2}}$, we multiply then by $5$ and we get $\displaystyle{-16\equiv 20a_2\pmod {4^2} \Rightarrow 0\equiv 4a_2 \pmod {4^2} \Rightarrow 4a_2\equiv 0\pmod {4^2}}$. We divide by $4$ and we get $\displaystyle{a_2\equiv 0\pmod {4}}$. The only residue of division by $4$ that solves this is $a_2=0$. Then we have $\displaystyle{\frac{1}{5}-1-3\cdot 4\equiv 4^3a_3 \pmod {4^4} \Rightarrow -\frac{4}{5}-3\cdot 4\equiv 4^3a_3\pmod {4^4}}$.
We divide by $4$ and we get $\displaystyle{-\frac{1}{5}-3\equiv 4^2a_3\pmod {4^3}\Rightarrow -\frac{16}{5}\equiv 4^2a_3 \pmod {4^3}}$, then we divide by $4^2$ and we get $\displaystyle{ -\frac{1}{5}\equiv a_3 \pmod 4}$. Then we multiply by $5$ and we get $\displaystyle{ -1\equiv 5a_3 \pmod 4\Rightarrow 5a_3\equiv -1 \pmod 4 \Rightarrow a_3\equiv 3 \pmod 4 }$. The only residue of division by $4$ that solves this is $a_3=1$.
Then we have $\displaystyle{\frac{1}{5}-1-3\cdot 4-4^3\equiv 4^4a_4 \pmod {4^5} \Rightarrow -\frac{4}{5}-3\cdot 4-4^3\equiv 4^4a_4\pmod {4^5}}$.
We divide by $4$ and get $\displaystyle{-\frac{1}{5}-3-4^2\equiv 4^3a_4\pmod {4^4}\Rightarrow -\frac{16}{5}-4^2\equiv 4^3a_4 \pmod {4^4}}$, then we divide by $4^2$ and get $\displaystyle{ -\frac{1}{5}-1\equiv 4a_4 \pmod 4^2 \Rightarrow -\frac{6}{5}\equiv 4a_4 \pmod {4^2}}$. We multiply then by $5$ and get $\displaystyle{ -6\equiv 20a_4 \pmod {4^2}\Rightarrow 20a_4\equiv -6 \pmod {4^2} \Rightarrow 4a_4\equiv 10 \pmod {4^2} }$.
This doesn't have a solution, right?
Where have I done something wrong? (Wondering)