- #1
BjornFanden
- 8
- 0
Hi,
I do not see how this method (illustrated in the figure below), can completely remove the 5th and 7th harmonic?
I know that in a wye-delta connection a 30 degree phase shift is introduced. But to fully remove the 5th harmonic we need a phase shift of 180/5 = 36, and for the 7th harmonic we need 180/7 = 25.71.
Since 36 and 25.71 degree is Close to 30 degree I assume they get greatly reduced. So parhaps they should not write "cancel out at the common bus" to avoid any confusion?
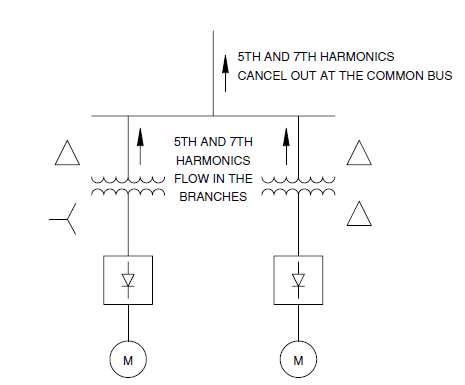
I do not see how this method (illustrated in the figure below), can completely remove the 5th and 7th harmonic?
I know that in a wye-delta connection a 30 degree phase shift is introduced. But to fully remove the 5th harmonic we need a phase shift of 180/5 = 36, and for the 7th harmonic we need 180/7 = 25.71.
Since 36 and 25.71 degree is Close to 30 degree I assume they get greatly reduced. So parhaps they should not write "cancel out at the common bus" to avoid any confusion?
Last edited: