dttah
- 37
- 0
Hello, I'd like to know if this is correct ... thank you.
You are given that the coefficient of kinetic friction between the block and the table in the attachment is 0.560, and m1 = 0.135 kg and m2 = 0.260 kg. (a) What should m3 be if the system is to move with a constant speed? (Assume ideal conditions for the string and pulleys.)
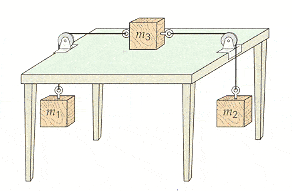
Start by writing down all of the forces involved in m1 and m2...
\Sigma F_{m1} = T_1 - m_1g = m_1a<br />
<br /> \Sigma F_{m2} = T_2 - m_2g = m_2a<br />
<br /> \Sigma F_{m3} = T_2 - T_1 - \mu m_3g = 0 <br />
I write = 0 because constant speed means no acceleration... so no acceleration means that F = ma => F = 0.
Now I have to solve this thingy, solve for T1 And T2 in the first two and stick it in the third.. getting..
<br /> T_1 = m_1g + m_1a<br />
<br /> T_2 = m_2g + m_2a<br />
<br /> m_2g + m_2a - m_1g - m_1a - \mu m_3g = 0<br />
Okie dokie, now we are able to solve for m3...
<br /> m_3 = \frac{m_2g + m_2a - m_1g - m_1a}{\mu g} \rightarrow \frac{m_2g - m_1g}{\mu g}
<br /> \frac{1,225}{5.488} = 0.2232
Homework Statement
You are given that the coefficient of kinetic friction between the block and the table in the attachment is 0.560, and m1 = 0.135 kg and m2 = 0.260 kg. (a) What should m3 be if the system is to move with a constant speed? (Assume ideal conditions for the string and pulleys.)
Homework Equations
The Attempt at a Solution
Start by writing down all of the forces involved in m1 and m2...
\Sigma F_{m1} = T_1 - m_1g = m_1a<br />
<br /> \Sigma F_{m2} = T_2 - m_2g = m_2a<br />
<br /> \Sigma F_{m3} = T_2 - T_1 - \mu m_3g = 0 <br />
I write = 0 because constant speed means no acceleration... so no acceleration means that F = ma => F = 0.
Now I have to solve this thingy, solve for T1 And T2 in the first two and stick it in the third.. getting..
<br /> T_1 = m_1g + m_1a<br />
<br /> T_2 = m_2g + m_2a<br />
<br /> m_2g + m_2a - m_1g - m_1a - \mu m_3g = 0<br />
Okie dokie, now we are able to solve for m3...
<br /> m_3 = \frac{m_2g + m_2a - m_1g - m_1a}{\mu g} \rightarrow \frac{m_2g - m_1g}{\mu g}
<br /> \frac{1,225}{5.488} = 0.2232