- #1
Rations
- 5
- 0
Hello. I'm wondering why my approach to solving this problem (Morin 3.2) is faulty.
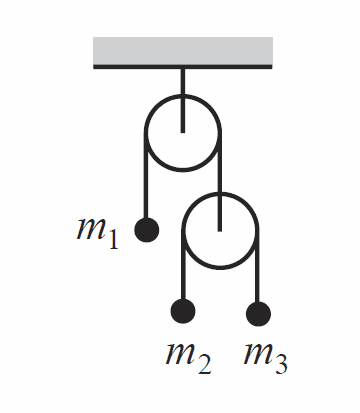
A double Atwood's machine is shown, with masses ##m_1##, ##m_2##, and ##m_3##. Find the accelerations of the masses.
##F = ma##
Let's say the string over the bottom pulley has tension ##T## and the string over the top pulley has tension ##T_2##. Assuming that the pulleys and ropes are massless and defining the upwards direction as positive, I have several equations:
(1) For ##m_1##: ##T_2 - m_1g = m_1a_1##
(2) For ##m_2##: ##T - m_2g = m_2a_2##
(3) For ##m_3##: ##T - m_3g = m_3a_3##
(4) For the lower pulley: ##T_2 - 2T = 0##
(5) From conservation of string: ##a_2 = -a_3##
If I substitute ##-a_3## into (2) and then solve (2) and (3) for ##T##, I find ##T = \frac{2m_2m_3g}{m_2 + m_3}##. From (4), ##T_2## is twice this value.
Then, I substitute my expression for ##T_2## into (1) and solve for ##a_1##, which yields:
[tex]a_1 = g\frac{4m_2m_3 - m_1(m_2 + m_3)}{m_1(m_2 + m_3)}[/tex]
This answer is close to what Morin writes, but is missing a term in the denominator. After reading his solution, which uses the fact that ##a_1 = -\left(\frac{a_2 + a_3}{2}\right)##, I feel that I can understand why his approach works. However, I do not see where I made a mistake.
Homework Statement
A double Atwood's machine is shown, with masses ##m_1##, ##m_2##, and ##m_3##. Find the accelerations of the masses.
Homework Equations
##F = ma##
The Attempt at a Solution
Let's say the string over the bottom pulley has tension ##T## and the string over the top pulley has tension ##T_2##. Assuming that the pulleys and ropes are massless and defining the upwards direction as positive, I have several equations:
(1) For ##m_1##: ##T_2 - m_1g = m_1a_1##
(2) For ##m_2##: ##T - m_2g = m_2a_2##
(3) For ##m_3##: ##T - m_3g = m_3a_3##
(4) For the lower pulley: ##T_2 - 2T = 0##
(5) From conservation of string: ##a_2 = -a_3##
If I substitute ##-a_3## into (2) and then solve (2) and (3) for ##T##, I find ##T = \frac{2m_2m_3g}{m_2 + m_3}##. From (4), ##T_2## is twice this value.
Then, I substitute my expression for ##T_2## into (1) and solve for ##a_1##, which yields:
[tex]a_1 = g\frac{4m_2m_3 - m_1(m_2 + m_3)}{m_1(m_2 + m_3)}[/tex]
This answer is close to what Morin writes, but is missing a term in the denominator. After reading his solution, which uses the fact that ##a_1 = -\left(\frac{a_2 + a_3}{2}\right)##, I feel that I can understand why his approach works. However, I do not see where I made a mistake.