- 860
- 365
We want to know the shortest distance from the point P to the line (see figure 1). As far as I know it is given by the length of the segment perpendicular to the line that joins the line to the point. Can you check this argument I give is correct?
Part A. First let us draw in the segment from the point P to the line that meets the line at 90 degrees (makes a right angle). We call this the perpendicular segment.
We call the point where the perpendicular segment meets the line Q (see figure 2).
Part B. IMPORTANT!:
We prove that the perpendicular segment represents the shortest distance from the point to the line by demonstrating that ANY OTHER SEGMENT from the point P to the line is longer!
Part C. To that end consider any point other than Q on the line, call it R. (see figure 3)
Part D. We draw in the segment from the point P to the point R.
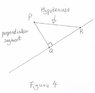
We notice that the points P,Q, and R are the corners of a right angled triangle where the segment from P to R is the hypotenuse and the perpendicular segment (from P to Q) is one of the other sides (see figure 4).
Part E. It is well known that the hypotenuse of a right angled triangle is the longest side. Thus we have proved that ANY OTHER SEGMENT is longer than the perpendicular segment.
Proof complete.
Part A. First let us draw in the segment from the point P to the line that meets the line at 90 degrees (makes a right angle). We call this the perpendicular segment.
We call the point where the perpendicular segment meets the line Q (see figure 2).
Part B. IMPORTANT!:
We prove that the perpendicular segment represents the shortest distance from the point to the line by demonstrating that ANY OTHER SEGMENT from the point P to the line is longer!
Part C. To that end consider any point other than Q on the line, call it R. (see figure 3)
Part D. We draw in the segment from the point P to the point R.
We notice that the points P,Q, and R are the corners of a right angled triangle where the segment from P to R is the hypotenuse and the perpendicular segment (from P to Q) is one of the other sides (see figure 4).
Part E. It is well known that the hypotenuse of a right angled triangle is the longest side. Thus we have proved that ANY OTHER SEGMENT is longer than the perpendicular segment.
Proof complete.