DreamWeaver
- 297
- 0
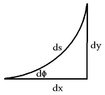
In the Euclidean plane, assume a differentiable function $$y=f(x)$$ exists. At any given point, say $$(x_0,y_0)$$, the line tangential to $$y=f(x)$$ at this point intersects the x-axis at an angle $$\phi$$.
The curvature of this curve, $$\kappa$$, is the rate of change of $$\phi$$ with respect to arc length, $$s$$:
$$\kappa = \frac{d\phi}{ds} $$Problem:Prove that
$$\kappa = \frac{ \left[ 1+ \left( \frac{dy}{dx} \right)^2 \right]^{3/2} }{ \frac{d^2y}{dx^2} }$$Or equivalently
$$\kappa = \frac{\left[ 1+\left( f'(x) \right)^2 \right]^{3/2}}{f''(x)}$$
The curvature of this curve, $$\kappa$$, is the rate of change of $$\phi$$ with respect to arc length, $$s$$:
$$\kappa = \frac{d\phi}{ds} $$Problem:Prove that
$$\kappa = \frac{ \left[ 1+ \left( \frac{dy}{dx} \right)^2 \right]^{3/2} }{ \frac{d^2y}{dx^2} }$$Or equivalently
$$\kappa = \frac{\left[ 1+\left( f'(x) \right)^2 \right]^{3/2}}{f''(x)}$$