- #1
Earthland
- 28
- 0
Homework Statement
In Cartesian coordinaate system, we describe the rotation of a cylinder. The axis of the cylinder has the same direction as the basis vector e3. Angular velocity is described by vector w = 2e1 - 5e2 + 7e3 rad/s. I must find the velocity vector (v) of a point P that is described by position vector OP = 1e2 + 3e3.
The Attempt at a Solution
I know the answer is just wXOP = (2,-5,7)X(0,1,3)=(-22,-6,2) and it's supposed to be an easy one. However, I can't quite imagine what is actually going on. I guess these are pretty stupid questions, but:
1) I know how the angular velocity vector is given. If the cylinder rotated around its axis, the angular velocity vector should be something like (0,0,x). Fine, cylinder don't have to rotate around its axis, but if so, doesn't the direction of the axis change and if so, what's the point of telling that its direction is e3?
2) A point on a cylinder would be moving so how can we describe it with a constant position vector? Or is it just a point "in space" through which the cylinder rotates?
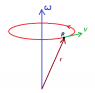
3) In case like this on the picture
I understand that angular velocity X position vector (r) would give right answer, since v must be perpendicular with both w and r. Well, that is just what wXr gives us, but in given task, w and position vector OP are not perpendicular to each other. They do define a plane to witch v can be perpendicular, but ... well I just don't get what it means.
If someone could draw me a picture, it would be most helpful.