Amaelle
- 309
- 54
- Homework Statement
- Show that the following sequence is convergent
- Relevant Equations
- Racine test
Good day
I have a question about the convergence of the following serie
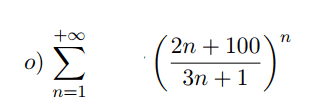
I understand that the racine test shows that it an goes to 2/3 which makes it convergent
but I also know that for a sequence to be convergent the term an should goes to 0 but the lim(n---->inf) ((2n+100)/(3n+1))^n)=lim exp(n*log(2n+100)/(3n+1))=+infinity
I'm really confused
thank you!
I have a question about the convergence of the following serie
I understand that the racine test shows that it an goes to 2/3 which makes it convergent
but I also know that for a sequence to be convergent the term an should goes to 0 but the lim(n---->inf) ((2n+100)/(3n+1))^n)=lim exp(n*log(2n+100)/(3n+1))=+infinity
I'm really confused
thank you!