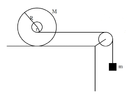
A question about a wheel rolling without slipping while tied to a cube
- Thread starter glen21082000
- Start date
Click For Summary
SUMMARY
The forum discussion centers on the mechanics of a wheel rolling without slipping while tied to a cube, specifically addressing torque calculations and the direction of friction. Users identify errors in the original solution, particularly the mislabeling of variables (R vs. r) and the need for clarity in the torque equation. The conversation emphasizes the importance of analyzing torques about the point of contact and understanding the implications of static friction in motion. Participants seek clarification on these concepts to better grasp the underlying physics.
PREREQUISITES- Understanding of basic physics concepts, particularly torque and friction.
- Familiarity with rotational dynamics and the equations of motion.
- Knowledge of inertial and non-inertial reference frames.
- Ability to interpret diagrams related to mechanical systems.
- Study the principles of torque and its calculation in rotational systems.
- Learn about static friction and its role in rolling motion.
- Explore the concept of inertial frames and their significance in mechanics.
- Review examples of similar mechanical systems to reinforce understanding of these principles.
Physics students, mechanical engineers, and educators seeking to deepen their understanding of rotational dynamics and friction in mechanical systems.