lorenz0
- 151
- 28
- Homework Statement
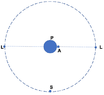
- Two moons (L), each of mass ##m##, rotate on the same circular orbit of radius ##10R## , around an exoplanet (P) of mass ##M## and radius ##R##.
The moons, shown in the figure, rotate counterclockwise and the planet's equator is on the plane of the orbit of the moons.
1. Determine the magnitude of the velocity ##v_L## of each moon.
A satellite (S), of mass ##m_s##, is launched from the equatorial point (A) of the planet,
at the instant shown in the figure, and positioned in the same circular orbit as the
moons, and rotates keeping equidistant from them. Find:
2. the energy that must be supplied to the satellite to place it in orbit;
3. the constant torque, with respect to the center of the orbit, which the satellite's motors must apply to allow the satellite to meet the moon that precedes it in the time it takes to do one revolution around the planet (remaining, by hypothesis, in the same circular orbit).
- Relevant Equations
- ##F_g=G\frac{m_1m_2}{R^2}##, ##F_{centr}=m\frac{v^2}{R}##
1) Considering the forces on one of the moons, I have: ##\frac{GMm}{(10R)^2}+\frac{Gm^2}{(20R)^2}=m\frac{v^2}{10R}\Leftrightarrow v=\sqrt{\frac{G}{10R}(M+\frac{m}{4})}.##
2) Considering the initial situation in which the satellite is at rest on the surface of the planet, ##E_i=-\frac{GMm_s}{R}-\frac{Gmm_s}{9R}-\frac{Gmm_s}{11R}=-\frac{20Gmm_s}{99R}## and a final situation in which the satellite is orbiting around the planet at a distance ##10R## equidistant from the moons, ##E_f=\frac{1}{2}m_sv^2-\frac{GMm_s}{10R}-2\frac{Gmm_S}{10\sqrt{2}R}=\frac{1}{2}mv^2-\frac{Gm_s}{10R}(M+\sqrt{2}m)## I have that the energy that has to be added is ##\Delta E=E_f-E_i=\frac{1}{2}m_sv^2-\frac{Gm_s(M+\sqrt{2}m)}{10R}+\frac{20Gmm_s}{99R}.## Now, considering the forces on the satellite in its final position I also have that ##\frac{Gm_s}{(10R)^2}(\frac{m}{\sqrt{2}}+M)=m_s\frac{v^2}{10R}\Leftrightarrow v=\sqrt{\frac{G}{10R}(\frac{m}{\sqrt{2}}+M)}## so ##\Delta E=E_f-E_i=\frac{1}{2}m_s(\frac{G}{10R}(\frac{m}{\sqrt{2}}+M))-\frac{Gm_s(M+\sqrt{2}m)}{10R}+\frac{20Gmm_s}{99R}.##
I still don't know how to do part (3) of the problem but I would like to know if I interpreted the problem in a correct way, i.e. the way I solved the first two parts of the problem makes sense. Thanks.
2) Considering the initial situation in which the satellite is at rest on the surface of the planet, ##E_i=-\frac{GMm_s}{R}-\frac{Gmm_s}{9R}-\frac{Gmm_s}{11R}=-\frac{20Gmm_s}{99R}## and a final situation in which the satellite is orbiting around the planet at a distance ##10R## equidistant from the moons, ##E_f=\frac{1}{2}m_sv^2-\frac{GMm_s}{10R}-2\frac{Gmm_S}{10\sqrt{2}R}=\frac{1}{2}mv^2-\frac{Gm_s}{10R}(M+\sqrt{2}m)## I have that the energy that has to be added is ##\Delta E=E_f-E_i=\frac{1}{2}m_sv^2-\frac{Gm_s(M+\sqrt{2}m)}{10R}+\frac{20Gmm_s}{99R}.## Now, considering the forces on the satellite in its final position I also have that ##\frac{Gm_s}{(10R)^2}(\frac{m}{\sqrt{2}}+M)=m_s\frac{v^2}{10R}\Leftrightarrow v=\sqrt{\frac{G}{10R}(\frac{m}{\sqrt{2}}+M)}## so ##\Delta E=E_f-E_i=\frac{1}{2}m_s(\frac{G}{10R}(\frac{m}{\sqrt{2}}+M))-\frac{Gm_s(M+\sqrt{2}m)}{10R}+\frac{20Gmm_s}{99R}.##
I still don't know how to do part (3) of the problem but I would like to know if I interpreted the problem in a correct way, i.e. the way I solved the first two parts of the problem makes sense. Thanks.