- #1
Leo Liu
- 353
- 156
- TL;DR Summary
- {##A_n##} is a sequence of positive numbers. ##\sum_{n=0}^{\infty} A_n(x-1)^n## has a R of convergence ##R=\frac 3 2##. Does ##\sum_{n=0}^{\infty} A_n## converge or diverge?
I tried to use the ratio test, but I am stuck on finding the range of the limit.
$$\because \left|x-1\right|<1.5=Radius$$
$$\therefore -0.5<x<2.5$$
$$\lim _{n \to \infty} \left| \frac{A_{n+1}(x-1)^{n+1}}{A_n(x-1)^n} \right|$$
$$\lim_{n \to \infty} \frac{A_{n+1} \left|x-1\right|}{A_n} <1$$
$$\lim_{n \to \infty} \left| \frac{A_{n+1}}{A_n} \right|< \frac 1 {\left| x-1 \right|}$$
Then I plotted the graph of 1/|x-1| and I found that the limit of A_n+1/A_n could vary from 2/3 (convergent) to infinity (divergent), as shown by the image below. What should I do next?
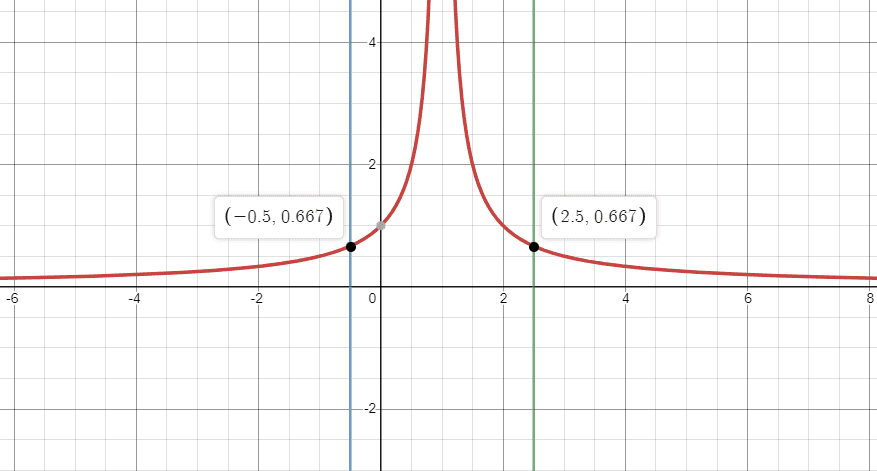
$$\because \left|x-1\right|<1.5=Radius$$
$$\therefore -0.5<x<2.5$$
$$\lim _{n \to \infty} \left| \frac{A_{n+1}(x-1)^{n+1}}{A_n(x-1)^n} \right|$$
$$\lim_{n \to \infty} \frac{A_{n+1} \left|x-1\right|}{A_n} <1$$
$$\lim_{n \to \infty} \left| \frac{A_{n+1}}{A_n} \right|< \frac 1 {\left| x-1 \right|}$$
Then I plotted the graph of 1/|x-1| and I found that the limit of A_n+1/A_n could vary from 2/3 (convergent) to infinity (divergent), as shown by the image below. What should I do next?
Last edited: