- #1
Ben9622111222
- 31
- 0
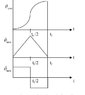
Hello,I have a setup which has a flexible rod that is rotated by a motor. The motor has encoder unit on it which gives the position in quad counts. This we can easily convert to degrees or radians. I have made many tests and the readings are perfect. So I used the plot of the position values and found the angular acceleration. This is convereted to m/s^2 by multiplying with the length of the rod. Though its a flexible rod and this is not valid, this would give me an idea.
At the same time, at the tip of the flexbile rod an accelerometer sensor is fixed and the acceleration at the tip is noted in m/s^2. These values are almost 1.5 to 1.8 times higher than the encoder calculated value. I have made many tests on the sensor as well and its is also working perfectly fine.
The question is that, if this is actually expected? Can tip acceleration be higher than at the axis? Can I trust my values?
If not, could anyone suggest or tip the reason for the higher values... Kindly reply.
At the same time, at the tip of the flexbile rod an accelerometer sensor is fixed and the acceleration at the tip is noted in m/s^2. These values are almost 1.5 to 1.8 times higher than the encoder calculated value. I have made many tests on the sensor as well and its is also working perfectly fine.
The question is that, if this is actually expected? Can tip acceleration be higher than at the axis? Can I trust my values?
If not, could anyone suggest or tip the reason for the higher values... Kindly reply.