Acceleration of objects connected by pulley on rough inclined plane

[songoku]

Summary:: Please see the picture below

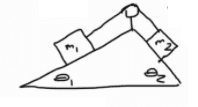
Let say:
$W_1$ is weight of $m_1$
$W_2$ is weight of $m_2$
$f_1$ is friction on $m_1$
$f_2$ is friction on $m_2$

I want to find the acceleration of the system. Since I don't know in which direction they will move, I just assume $m_1$ will move downward, so

$$a=\frac{W_1 \sin \theta_1-W_2 \sin \theta_2 -f_1-f_2}{m_1+m_2}...(1)$$

If the value of $a$ is negative, this means that actually $m_1$ moves upward.

My teacher said the value of the acceleration will be the same, just the direction will be opposite. But when I tried doing it, I didn't reach that conclusion.

If $m_1$ moves upward:
$$a=\frac{W_2 \sin \theta_2-W_1 \sin \theta_1 -f_1-f_2}{m_1+m_2}...(2)$$

Equation (2) is not negative of equation (1)

Where is my mistake? Thanks

 

[A.T.]

My teacher said the value of the acceleration will be the same,

It has to be, if the string doesn't stretch.

Where is my mistake? Thanks

You only need one equation because there is only one acceleration. Combining Equations (1) and (2) makes no sense, because they use different sign conventions. Use (1) or (2).

 

[songoku]

I just tried with random number. Let say:
$m_1$ = 10 kg
$m_2$ = 5 kg
$\theta_1=30^0$
$\theta_2 = 45^0$
$\mu_k=0.1$ for both objects

1) I assume $m_1$ moves upwards
Equation for $m_1$:
$$\Sigma F=m.a$$
$$T-m_1.g \sin \theta_1 - \mu_k . m_1.g \cos \theta_1 = m_1.a$$
$$T=10a+57.546$$

Equation for $m_2$:
$$\Sigma F=m.a$$
$$m_2.g \sin \theta_2 - T - \mu_k.m_2.g \cos \theta_2 = m_2.a$$
$$34.6836-10a-57.546-31.215=5a$$
$$a=-3.61 ms^{-2}$$

Since the acceleration is negative, $m_1$ actually moves downwards and I redo the working, changing the direction of friction and expecting to get $a=3.61 ms^{-2}$

2) $m_1$ actually moves downwards
Equation for $m_1$:
$$\Sigma F = m.a$$
$$m_1 .g \sin \theta_1 - T - \mu_k .m_1 .g \cos \theta_1=m_1.a$$
$$T=40.554 - 10a...(1)$$

Equation for $m_2$:
$$\Sigma F=m_2.a$$
$$T - m_2.g \sin \theta_2 - \mu_k . m_2.g \cos \theta_2=m_2.a$$
$$40.554 -10a-34.6836-3.4684=5a$$
$$a=0.16~ms^{-2}$$

I do not get 3.61 ms^-2, like what I expect when getting the negative acceleration. That's why I think if I get negative value for acceleration, I need to redo all my working, not simply use the same magnitude of acceleration.

Something wrong with my working? Thanks

 

[haruspex]

Where is my mistake?

Your mistake is in undue trust in your teacher's remarks.

When there's a frictional force that could act either way involved, you cannot just suppose the acceleration to be in one direction then, on getting a negative answer, just assume that is the right magnitude but the acceleration has opposite direction from what you supposed.

E.g. consider the case in which the two W sin terms nearly balance and the max frictional forces are enough to hold matters static. Whichever way you suppose it slips you will get a negative answer.

 

[Lnewqban]

...
If the value of $a$ is negative, this means that actually $m_1$ moves upward.

You could assume that with a velocity, but not with a rate of change, which is what an acceleration is.
Negative rate always means that the value is decreasing.
A negative acceleration always means that the mass is slowing down.

I like to simplify this type of problems as two masses sliding on a horizontal surface, while attached to each other by a string.

 

[songoku]

Thank you very much A.T. , haruspex, Lnewqban