Acceleration Vectors: Calculating Average Acceleration in a Direction Change

In summary, a soccer player running at a speed of 4.0 m/s changes his direction by 30.0o and takes 3.0s to do so. To find his average acceleration during the turn, you can use the equation a = v / t. The triangle in the attachment can be used to break down the velocity into components and solve for the average acceleration. The speed is assumed to be constant at 4.0 m/s.
  • #1
GodOfYou
4
0

Homework Statement



A Soccer player is running down the field with a ball at a speed of 4.0 m/s. He cuts to the right at an angle of 30.0o to his original direction to receive a pass. If it takes him 3.0s to change is direction, what is his average acceleration during the turn?

Homework Equations



a = v / t

a2+b2=c2

Sin, Cos, Tan ex. Cos 45o = delta d1 / delta d2


The Attempt at a Solution



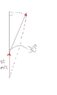
I have drawn the triangle In attachment.
The dotted lines are me making the triangle.

Then I broke the top triangle into a right angle triangle (in second attachment)

and now I am stuck.. I have never worked with angles in this type of problem and I need help.

Thanks,
Jason
 

Attachments

  • main triangle.jpg
    main triangle.jpg
    7.2 KB · Views: 364
  • first triangle.jpg
    first triangle.jpg
    5.9 KB · Views: 365
Physics news on Phys.org
  • #2
Break both his old and new velocity into components.
 
  • #3
so when he turns to the right he will still be moving at 4.0 m/s?
 
  • #4
Yes, it looks like we are supposed to assume the speed is still 4.0 m/s after the turn.
 

FAQ: Acceleration Vectors: Calculating Average Acceleration in a Direction Change

1. What is an acceleration vector?

An acceleration vector is a mathematical representation of the change in an object's velocity over time. It includes both the direction and magnitude of the change in velocity.

2. How is an acceleration vector calculated?

An acceleration vector can be calculated by dividing the change in velocity by the change in time. This is known as the average acceleration formula: a = (vf - vi)/Δt, where a is acceleration, vf is final velocity, vi is initial velocity, and Δt is change in time.

3. What is the difference between acceleration and velocity?

Acceleration is the rate of change of velocity, while velocity is the rate of change of an object's position. In simpler terms, acceleration is how fast an object's speed is changing, while velocity is how fast an object is moving in a particular direction.

4. How do acceleration vectors help in understanding motion?

Acceleration vectors help in understanding motion by providing a visual representation of how an object's velocity is changing over time. They can also be used to calculate the acceleration of an object, which is essential in understanding the forces acting on the object and predicting its future motion.

5. What are some real-life examples of acceleration vectors?

Some real-life examples of acceleration vectors include a car accelerating from a stop, a roller coaster going down a steep incline, and a rocket launching into space. In each of these scenarios, the acceleration vector shows the direction and magnitude of the change in velocity over time.

Similar threads

I need some clarification for a high school vectors question (accelerating bird)
Replies
14
Views
1K
Vectors, how to find average acceleration
Replies
13
Views
6K
Acceleration Vector Word Problem
Replies
4
Views
2K
Direction of vector acceleration in circular motion
Replies
13
Views
2K
Finding the resultant of three vectors
Replies
20
Views
11K
Adding Vectors: Understanding Direction and Length
Replies
5
Views
1K
Average acceleration of the a particle in circular motion
Replies
16
Views
10K
Direction of car's average acceleration vector as it turns
Replies
8
Views
7K
Vector addition and the force applied to the shaft of the pulley
Replies
4
Views
2K
Finding magnitude of vector without direction (kite problem)
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top