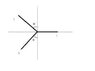
aek said:
Can someone tell me how to add these 3 vectors to show that they all add up to zero. Even though there is 3 vectors somehow there is 5, don't really understand. The diagram is drawn below.If unclear, the two angles are 30 degrees and each length is 1. Thanks in advance.
I have no idea what you mean by "even though there is 3 vectors somehow there is 5"!
One problem is that neither your diagram nor your description tells us in which of the two possible directions the vectors go. However, in order for them to cancel (add to 0), the vectors on the left must point to the left, the one on the right, to the right.
It should be clear from symmetry that the two vectors on the left, one going up at 30 degrees, the other down at 30 degrees will cancel
vertically- that is the sum will on the horizontal axis.
The way of calculating that, as well as calculating the length of the vector
sum of the two on the left is to use trigonometry. The vector pointing to the left and upward forms a right triangle with the horizontal axis with angle 30 degrees and hypotenuse 1. Since sine is "opposite over hypotenuse",
sin(30)= y/1= y where y is the vertical component of the vector. Since cosine is "near side over hypotenuse", cos(30)= x/1 where x is the horizontal component of the vector.
Since the other left pointing vector has the same angle, you will get exactly the same vertical and horizontal values- except that since one is pointing up and the other pointing down, the vertical components will cancel while the horizontal will add. If you find cos(30) you should see immediately why the sum of those two will cancel the third, horizontal, vector.