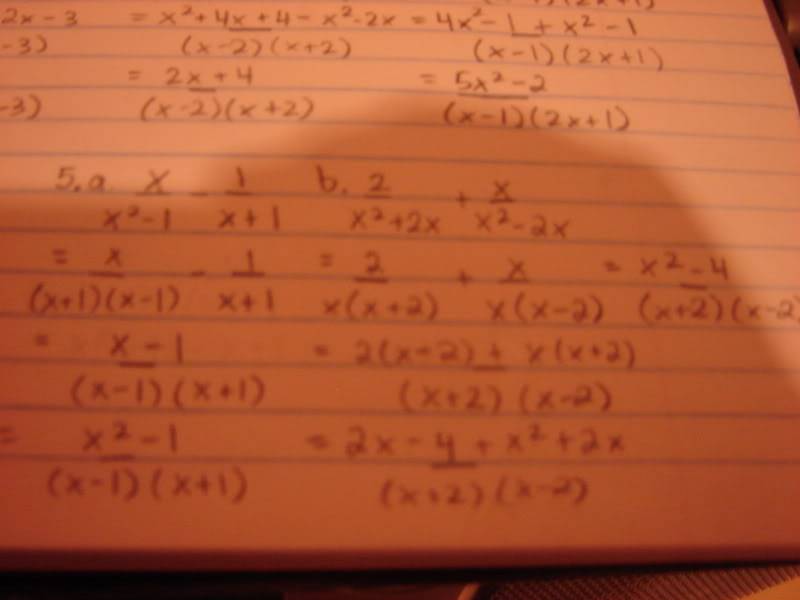SUMMARY
The discussion focuses on the addition and subtraction of rational expressions, specifically addressing the error in combining fractions. The correct expression for the problem presented is 3x + 2/(x+2)(x-2). A mistake was identified in the calculation of the expression \frac{2}{x(x+2)} + \frac{x}{x(x-2)}, which was incorrectly simplified. The importance of proper notation in mathematical expressions was also emphasized, particularly the need for the fraction bar to extend over both the numerator and denominator.
PREREQUISITES
- Understanding of rational expressions
- Knowledge of fraction addition and subtraction techniques
- Familiarity with algebraic manipulation
- Ability to identify and correct mathematical errors
NEXT STEPS
- Study the rules for adding and subtracting rational expressions
- Practice simplifying complex fractions
- Learn about the importance of proper notation in mathematical writing
- Explore common mistakes in algebraic expressions and how to avoid them
USEFUL FOR
Students learning algebra, educators teaching rational expressions, and anyone seeking to improve their mathematical notation and error-checking skills.