- #1
MisterP
- 47
- 3
- Homework Statement
- Hello. Could someone help me?
I have to:
1) from given harmonics syntesize signal
2) calculate effective value of signal
3) represent resultant signal
Specs:
I assume frequency is 50hz
Table given below
- Relevant Equations
- A0/2 + A1*cos ("what goes here?" + Fi1) + etc..
Formula I have shows is probably for resulting harmonic? Does syntesizing mean writing the main formula? I havo no clue about effective value of signal and representation is probably done in excel or other graphing app.
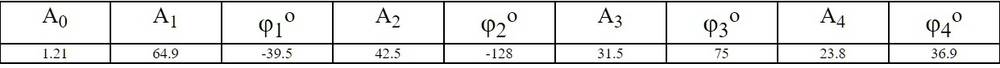
Last edited by a moderator: