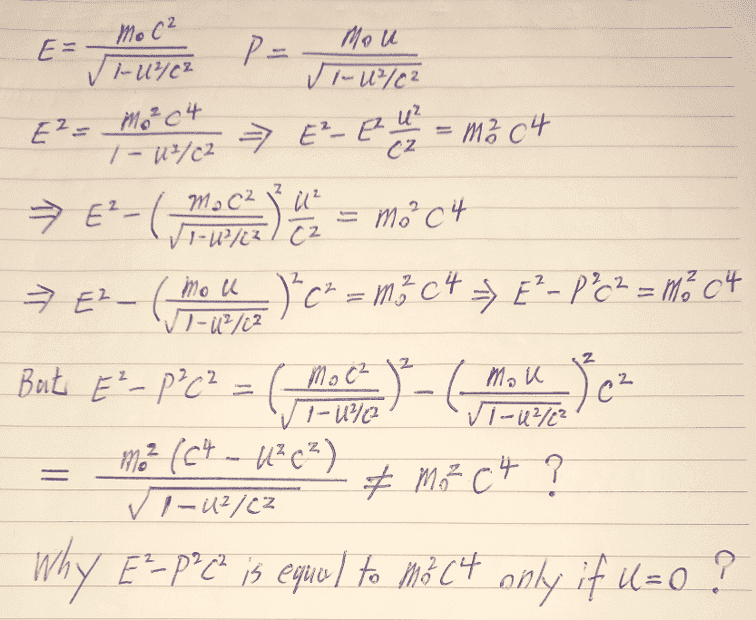SUMMARY
The discussion centers on the algebraic manipulation of the energy-momentum relationship, specifically the equation $$E^2 - p^2 c^2 = \gamma^2m^2c^4(1 - \frac{v^2}{c^2})$$. Participants identified errors in the calculation, particularly the misuse of square roots after squaring terms. The correct interpretation leads to the conclusion that the expression in brackets simplifies to $$\frac{1}{\gamma^2}$$, clarifying the relationship between energy, momentum, and relativistic mass.
PREREQUISITES
- Understanding of the energy-momentum relationship in physics
- Familiarity with algebraic manipulation of equations
- Knowledge of relativistic concepts such as gamma factor ($$\gamma$$)
- Basic understanding of the speed of light ($$c$$) in physics
NEXT STEPS
- Study the derivation of the energy-momentum relationship in special relativity
- Learn about the gamma factor ($$\gamma$$) and its implications in relativistic physics
- Explore algebraic techniques for manipulating complex equations
- Investigate common pitfalls in algebraic calculations within physics
USEFUL FOR
Students of physics, educators teaching relativity, and anyone interested in mastering algebraic operations in the context of energy-momentum relationships.