Alpha Particle Scattering and angular momentum

[brotherbobby]

Statement of the problem :

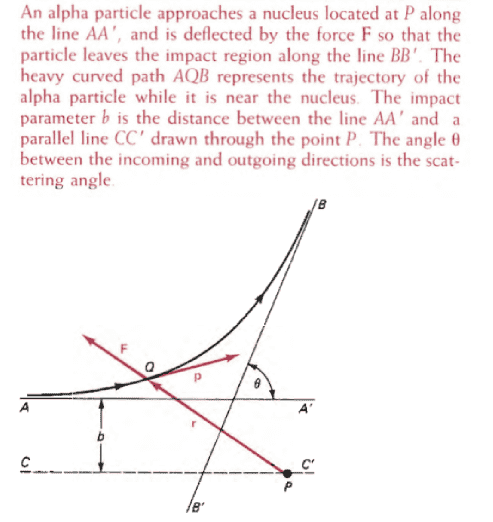
"Using the definition L = r $\times$ p, prove that the direction of L is constant for an alpha ($\alpha$) particle whose scattering is shown in the diagram below. "

Relevant equations :

We are aware that the scattering takes place via a central force F = F(r) $\hat r$. Angular momentum L = r $\times$ p and torque $\tau = r \times F$ (all vectors)The attempt at a solution

I can solve the problem, but not the way it asks. The torque $\tau = r \times F \Rightarrow \tau = 0$ since the force is central : F = F(r) $\hat r$. Using $\tau = \frac{dL}{dt} = 0$, inplies that the angular momentum vector L is constant.

[This is not what the question asks for. It asks to show only the direction of L conserved, from the definition of L : L = r $\times$ p].

 

[Orodruin]

If the vector itself is constant, then its direction must be conserved too ...

Also, where do you think $\vec \tau = \vec r \times \vec F$ comes from?

 

[brotherbobby]

If the vector itself is constant, then its direction must be conserved too ...

Yes, in that sense I have answered the question, but as I said, not in the way they asked for. I suppose they want one to focus on the direction of L and show that it remains the same.

Also, where do you think →τ=→r×→Fτ→=r→×F→\vec \tau = \vec r \times \vec F comes from?

I don't know. Torque and angular momentum are definitions, defined as the cross product of the radius vector and the force or the linear momentum, respectively.

 

[Orodruin]

Torque and angular momentum are definitions, defined as the cross product of the radius vector and the force or the linear momentum, respectively.

So you need to relate those two, which you are going to do by computing the time derivative of the angular momentum.

 

[brotherbobby]

So you need to relate those two, which you are going to do by computing the time derivative of the angular momentum.

All I am aware of is the standard : $\frac{dL}{dt} = \frac{d}{dt}(r \times p) = r \times \frac{dp}{dt} = r \times F$.

It is this that I used to answer why the angular momentum L is constant - viz. the thrque is 0 owing to the fact that the force is central and hence L remains the same.

But the question asks me to show that the direction of L is a constant for a central force like this. (I am aware that I have already shown this in the form of the vector L itself being a constant).

I wonder if there is another way.

For instance, a vector L = $L\hat L$. Can we show that $\hat L$ is a constant from the definition of L ( = $r \times p$) for a central force (F(r))?