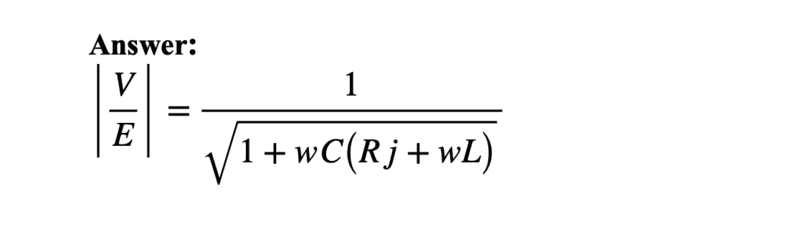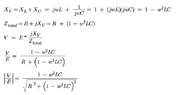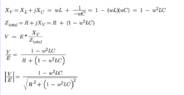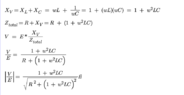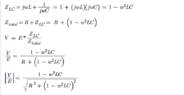SUMMARY
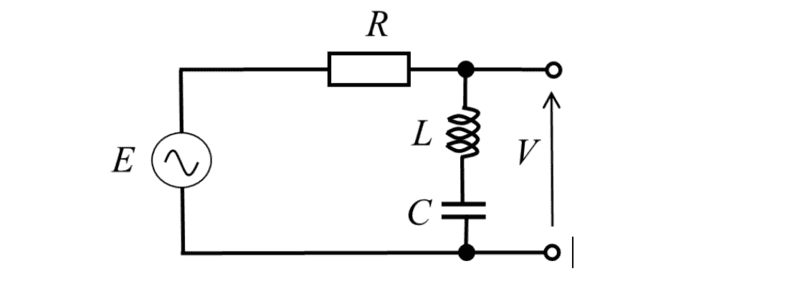
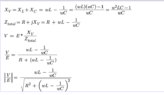
The discussion focuses on the analysis of analog filter circuits, specifically addressing the calculation of reactance in RLC circuits. Key concepts include the total impedance formula Ztotal = R + jXv, where Xv = XL + XC, and the importance of correctly identifying the signs of reactance for capacitors and inductors. The conversation emphasizes the necessity of maintaining the orthogonality of real and imaginary components in complex impedance calculations, particularly at resonance where reactance equals zero.
PREREQUISITES
- Understanding of RLC circuit theory
- Familiarity with complex numbers and impedance
- Knowledge of reactance formulas: XL = ωL and XC = -1/ωC
- Basic principles of resonance in electrical circuits
NEXT STEPS
- Study complex impedance calculations in electrical engineering
- Learn about resonance and its effects in RLC circuits
- Explore the significance of reactance signs in circuit analysis
- Review advanced topics in electrical reactance and filter design
USEFUL FOR
Electrical engineering students, circuit designers, and anyone involved in the analysis and design of analog filters will benefit from this discussion.