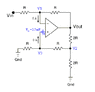
Discussion Overview
The discussion revolves around the analysis of an operational amplifier (OPAMP) circuit that includes an input offset voltage. Participants explore the implications of this offset voltage on the output voltage calculations, utilizing concepts such as superposition and nodal analysis. The scope includes homework-related problem-solving and mathematical reasoning regarding circuit behavior.
Discussion Character
- Homework-related
- Mathematical reasoning
- Technical explanation
- Debate/contested
Main Points Raised
- One participant presents an approach to calculate output voltage using superposition, considering both input voltage and offset voltage.
- Another participant suggests that the gain of the circuit may differ from standard formulas due to resistor values, prompting a discussion on the need for nodal analysis.
- Some participants question whether the standard inverting and non-inverting equations apply, indicating that adjustments may be necessary based on the actual circuit configuration.
- There is a suggestion to analyze the circuit from scratch rather than relying on derived equations, emphasizing the importance of understanding the influence of each component.
- One participant expresses uncertainty about how to handle multiple input voltages at the OPAMP terminals and considers using a different reference point for calculations.
- Another participant warns that changing the ground reference could complicate the analysis, as it would affect all interconnected points in the circuit.
- Some participants reflect on the limitations of cookie-cutter formulas and the necessity of being able to analyze non-standard circuits effectively.
- A later reply acknowledges an error in an intuitive formula derived by one participant, reinforcing the value of deriving formulas directly.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the best approach to analyze the OPAMP circuit. There are competing views on whether to adjust existing gain equations or derive new ones, and uncertainty remains regarding the handling of input voltages and reference points.
Contextual Notes
Some participants note that the resistor values in the circuit may not match those of standard configurations, which could affect the applicability of derived equations. Additionally, the discussion highlights the interconnectedness of circuit components and the potential complications arising from changing reference points.
Who May Find This Useful
This discussion may be useful for students studying operational amplifiers, circuit analysis, and those seeking to understand the implications of input offset voltage in practical applications.