etf
- 179
- 2
Here is my task (Basics of analogue telecommunications):
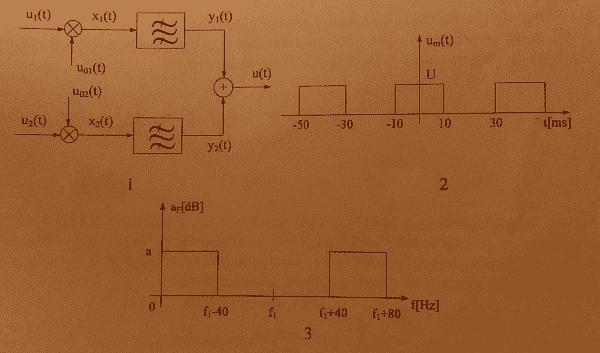
Block diagram of device for simultaneous transfer of two telegraphic signals u1(t) and u2(t) is shown on image 1. Both signals have waveform as periodioc signal um(t) on image 2. Frequencies f1 and f2 of carriers $$u_{01}(t)=U_0 cos(\omega_1 t)$$ and $$u_{02}(t)=U_0 cos(\omega_2 t)$$ are choosen so f2=f1+120Hz.
For good transfer of telegraphic signal through one channel it is enough to transfer components in range of 80Hz around frequency of carrier. For that purpose, bandpass filter in first channel has attenuation characteristic as in image 3. Characteristic of attenuation of filter in second channel has same shape, only it is shifted to right for 120Hz.
Because of finite attenuation of filter in stop band, signal u(t) contains unwanted products of modulation, some of which fall from one channel in bandpass of second channel. If condition is that logarithmic ratio of median power of whole signal and median power of parasitic components in one channel equals 40dB, calculate attenuation of filter, a[dB], in stop band.
Any suggestion?
We are studying amplitude, phase and frequency modulations now. Although I'm familiar with basic concepts, I don't know how to apply it here.
I wrote signal um(t) in terms of Fourier series. x1(t) would be Fourier series of um(t) times carrier u01(t), and x2(t) would be Fourier series of um(t) times carrier u02(t).
Final result is a = 19.5 dB
Block diagram of device for simultaneous transfer of two telegraphic signals u1(t) and u2(t) is shown on image 1. Both signals have waveform as periodioc signal um(t) on image 2. Frequencies f1 and f2 of carriers $$u_{01}(t)=U_0 cos(\omega_1 t)$$ and $$u_{02}(t)=U_0 cos(\omega_2 t)$$ are choosen so f2=f1+120Hz.
For good transfer of telegraphic signal through one channel it is enough to transfer components in range of 80Hz around frequency of carrier. For that purpose, bandpass filter in first channel has attenuation characteristic as in image 3. Characteristic of attenuation of filter in second channel has same shape, only it is shifted to right for 120Hz.
Because of finite attenuation of filter in stop band, signal u(t) contains unwanted products of modulation, some of which fall from one channel in bandpass of second channel. If condition is that logarithmic ratio of median power of whole signal and median power of parasitic components in one channel equals 40dB, calculate attenuation of filter, a[dB], in stop band.
Any suggestion?
We are studying amplitude, phase and frequency modulations now. Although I'm familiar with basic concepts, I don't know how to apply it here.
I wrote signal um(t) in terms of Fourier series. x1(t) would be Fourier series of um(t) times carrier u01(t), and x2(t) would be Fourier series of um(t) times carrier u02(t).
Final result is a = 19.5 dB