vw17
- 1
- 0
Hi,
I'd to work with a model which represents a contact problem. I want to suppose that f_0=0 and f_2=0 where f_0 is a density of body forces and f_2 is a density of surface tractions .
I am mathematician so I don't know if the hypothesis that I'd to suppose will make the problem have a sense in physics or no?
the problem is attached below (pdf).
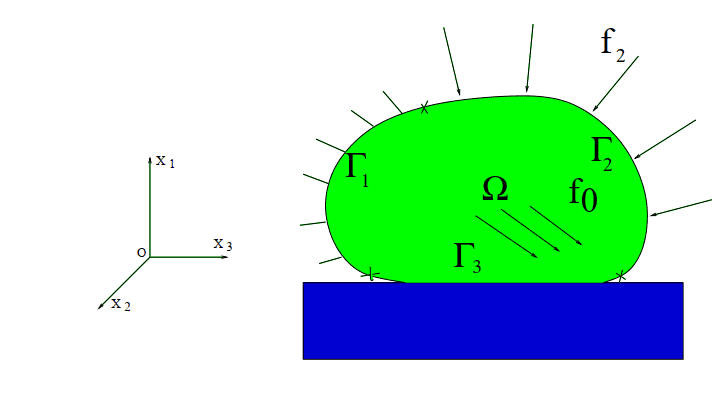
I'd to work with a model which represents a contact problem. I want to suppose that f_0=0 and f_2=0 where f_0 is a density of body forces and f_2 is a density of surface tractions .
I am mathematician so I don't know if the hypothesis that I'd to suppose will make the problem have a sense in physics or no?
the problem is attached below (pdf).
Attachments
Last edited by a moderator: